Zadanie nr 9261993
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 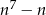 jest podzielna przez 7.
jest podzielna przez 7.
Rozwiązanie
Sposób I
Rozkładamy podane wyrażenie
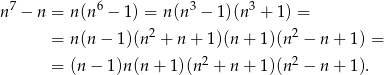
Jeżeli liczba  daje przy dzieleniu przez 7 resztę 1, 0 lub 6, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 7. Pozostało zająć się sytuacją, gdy liczba
daje przy dzieleniu przez 7 resztę 1, 0 lub 6, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 7. Pozostało zająć się sytuacją, gdy liczba  przy dzieleniu przez 7 daje resztę 2, 3, 4 lub 5. Zauważmy, że jeżeli
przy dzieleniu przez 7 daje resztę 2, 3, 4 lub 5. Zauważmy, że jeżeli 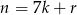 to
to
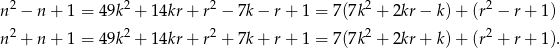
Łatwo teraz sprawdzić, że jeżeli 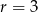 lub
lub 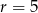 to pierwsze wyrażenie dzieli się przez 7, a jeżeli
to pierwsze wyrażenie dzieli się przez 7, a jeżeli 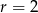 lub
lub 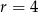 to drugie wyrażenie jest podzielne przez 7.
to drugie wyrażenie jest podzielne przez 7.
Sposób II
Postępujemy jak poprzednio, ale używamy odrobinę sprytniejszego rozkładu.
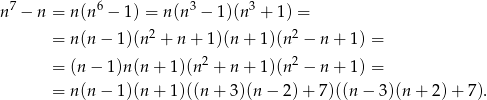
Zauważmy teraz, że 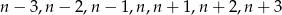 to 7 kolejnych liczb całkowitych, więc jedna z nich na pewno dzieli przez 7. To oznacza, że wyrażenie w jednym z powyższych nawiasów jest liczbą podzielną przez 7.
to 7 kolejnych liczb całkowitych, więc jedna z nich na pewno dzieli przez 7. To oznacza, że wyrażenie w jednym z powyższych nawiasów jest liczbą podzielną przez 7.
Sposób III
Jest jasne, że przez 7 dzieli się liczba
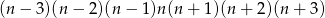
(bo wśród 7 kolejnych liczb całkowitych zawsze jedna dzieli się przez 7). Wymnóżmy ten iloczyn i sprawdźmy, czym różni się on od 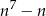 . Liczymy
. Liczymy
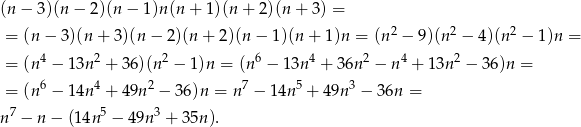
Zatem
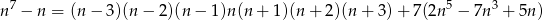
i widać, że rzeczywiście 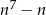 zawsze dzieli się przez 7.
zawsze dzieli się przez 7.
Sposób IV
Zadanie możemy też rozwiązać indukcyjnie, ale będziemy potrzebować wzoru dwumianowego Newtona dla 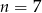
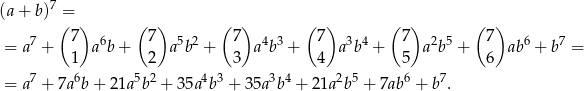
Zakładamy indukcyjnie, że 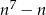 dzieli się przez 7 i liczymy
dzieli się przez 7 i liczymy
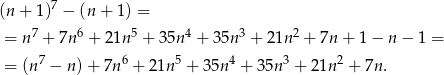
Wyrażenie w nawiasie dzieli się przez 7 z założenia indukcyjnego, reszta też, więc wykazaliśmy tezę dla 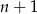 .
.
Zadanie jest szczególnym przypadkiem tzw. małego twierdzenia Fermata: jeżeli 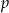 jest liczbą pierwszą, to
jest liczbą pierwszą, to 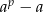 dzieli się przez
dzieli się przez 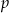 .
.

