Zadanie nr 9399626
Dana jest liczba całkowita 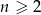 . Niech
. Niech 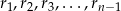 będą odpowiednio resztami z dzielenia liczb
będą odpowiednio resztami z dzielenia liczb
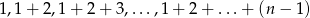
przez  . Znaleźć wszystkie takie wartości
. Znaleźć wszystkie takie wartości  , że ciąg
, że ciąg 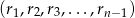 jest permutacją ciągu
jest permutacją ciągu 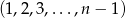 .
.
Rozwiązanie
Dla prostoty nie będziemy odróżniać ciągu
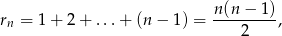
od ciągu reszt jakie dają te liczby przy dzieleniu przez  (
( będziemy mieli cały czas ustalone, więc nie prowadzi to do nieporozumień).
będziemy mieli cały czas ustalone, więc nie prowadzi to do nieporozumień).
Po pierwsze wypisujemy sobie pierwszych kilka (kilkanaście) początkowych wyrazów ciągu 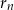 i patrzymy dla jakich
i patrzymy dla jakich  ciągi reszt są takie jak powinny być. Jak się to zrobi to narzuca się odpowiedź – będzie OK tylko dla potęg 2, czyli liczb postaci
ciągi reszt są takie jak powinny być. Jak się to zrobi to narzuca się odpowiedź – będzie OK tylko dla potęg 2, czyli liczb postaci 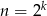 . Ponadto dla liczb nieparzystych ostatnia reszta
. Ponadto dla liczb nieparzystych ostatnia reszta 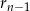 dzieli się przez
dzieli się przez  . Spróbujmy to uzasadnić.
. Spróbujmy to uzasadnić.
Jeżeli 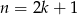 jest nieparzyste to sprawa jest prosta
jest nieparzyste to sprawa jest prosta
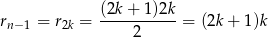
i widać, że liczba ta jest podzielna przez  (a więc nie należy do zbioru
(a więc nie należy do zbioru 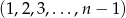 )
)
O zadaniu trzeba myśleć następująco: ciąg reszt będzie żądaną permutacją, jeżeli każde dwie reszty będą różne. Aby tak było wystarczy, że 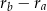 nie dzieli się przez
nie dzieli się przez  dla
dla 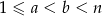 . Ze wzoru na sumę ciągu arytmetycznego mamy
. Ze wzoru na sumę ciągu arytmetycznego mamy
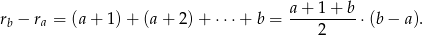
Załóżmy najpierw, że  ma czynnik nieparzysty, czyli jest postaci
ma czynnik nieparzysty, czyli jest postaci 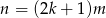 i
i 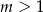 . Spróbujmy dobrać
. Spróbujmy dobrać  i
i 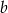 , żeby różnica reszt wyszła podzielna przez
, żeby różnica reszt wyszła podzielna przez  . Trochę kombinując, można to wymyślić:
. Trochę kombinując, można to wymyślić:
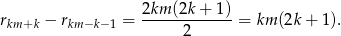
W powyższej równości jest jeden drobny detal, mianowicie dla 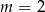 i
i 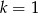 mamy
mamy 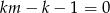 , ale przypadek
, ale przypadek 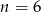 możemy rozważyć osobno (lub przyjąć, że
możemy rozważyć osobno (lub przyjąć, że 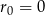 ).
).
Pozostało zastanowić się nad przypadkiem 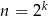 . Zastanówmy się czy liczba
. Zastanówmy się czy liczba
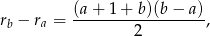
gdzie 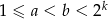 , może dzielić się przez
, może dzielić się przez 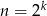 . Zauważmy, że tylko jedna z liczb
. Zauważmy, że tylko jedna z liczb 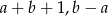 jest parzysta i w dodatku maksymalnie może dzielić się przez
jest parzysta i w dodatku maksymalnie może dzielić się przez 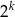 (bo obie liczby są mniejsze od
(bo obie liczby są mniejsze od 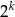 , więc oba wyrażenia są mniejsze od
, więc oba wyrażenia są mniejsze od 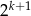 ). Zatem liczba
). Zatem liczba
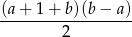
nie dzieli się przez potęgę 2 wyższą niż 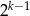 , co kończy dowód.
, co kończy dowód.

