Zadanie nr 9401725
Dane są różne liczby pierwsze 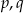 oraz takie dodatnie liczby całkowite
oraz takie dodatnie liczby całkowite 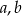 , że liczba
, że liczba 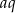 daję resztę 1 przy dzieleniu przez
daję resztę 1 przy dzieleniu przez 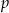 , a liczba
, a liczba 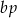 daje resztę 1 przy dzieleniu przez
daje resztę 1 przy dzieleniu przez 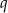 . Wykaż, że
. Wykaż, że
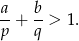
Rozwiązanie
Wiemy, że 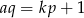 i
i 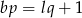 dla pewnych liczb naturalnych
dla pewnych liczb naturalnych 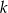 i
i 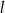 . To oznacza, że
. To oznacza, że
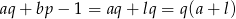
oraz
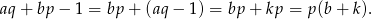
To oznacza, że liczba 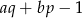 dzieli się zarówno przez
dzieli się zarówno przez 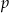 jak i przez
jak i przez 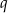 . W takim razie dzieli się też przez
. W takim razie dzieli się też przez 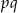 (bo
(bo 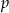 i
i 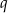 są dwoma różnymi liczbami pierwszymi). Zatem
są dwoma różnymi liczbami pierwszymi). Zatem