Zadanie nr 9461216
Wyznacz wszystkie liczby pierwsze 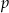 takie, że liczby
takie, że liczby 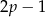 i
i 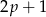 też są liczbami pierwszymi.
też są liczbami pierwszymi.
Rozwiązanie
Zauważmy, liczby 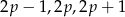 są trzema kolejnymi liczbami całkowitymi, więc jedna z nich dzieli się przez 3.
są trzema kolejnymi liczbami całkowitymi, więc jedna z nich dzieli się przez 3.
Jeżeli 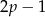 dzieli się przez 3, to
dzieli się przez 3, to 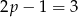 bo ma to być liczba pierwsza. Zatem
bo ma to być liczba pierwsza. Zatem 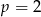 i
i 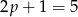 też jest liczbą pierwszą.
też jest liczbą pierwszą.
Jeżeli 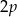 dzieli się przez 3, to musi być
dzieli się przez 3, to musi być 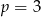 . Wtedy
. Wtedy 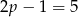 i
i 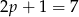 też są liczbami pierwszymi.
też są liczbami pierwszymi.
Jeżeli wreszcie 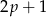 dzieli się przez 3, czyli
dzieli się przez 3, czyli 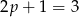 to
to 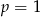 – nie jest to jednak liczba pierwsza.
– nie jest to jednak liczba pierwsza.
Odpowiedź: 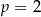 lub
lub