Zadanie nr 1431230
Udowodnij, że dla każdej liczby nieparzystej 
wyrażenie 
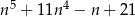jest podzielne przez 16.
Rozwiązanie
Sposób I
Zauważmy najpierw, że
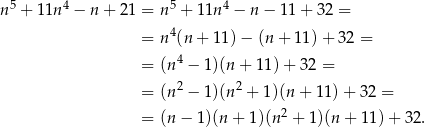
Teraz wystarczy zauważyć, że jeżeli 
jest liczbą nieparzystą, to w każdym z czterech pierwszych nawiasów mamy liczbę parzystą, więc iloczyn tych nawiasów jest podzielny przez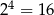 
. To oczywiście oznacza, że cała liczba też jest podzielna przez 16.
Sposób II
Zauważmy najpierw, że
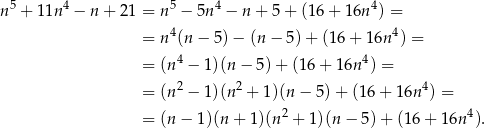
Teraz wystarczy zauważyć, że jeżeli 
jest liczbą nieparzystą, to w każdym z czterech pierwszych nawiasów mamy liczbę parzystą, więc iloczyn tych nawiasów jest podzielny przez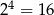 
. To oczywiście oznacza, że cała liczba też jest podzielna przez 16.
