Zadanie nr 2370050
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
Rozwiązanie
Oznaczmy dwie kolejne liczby nieparzyste przez 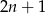 i
i 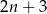 . Wtedy
. Wtedy
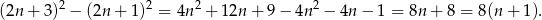
Widać, że jest to liczba podzielna przez 8.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
Oznaczmy dwie kolejne liczby nieparzyste przez 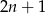 i
i 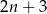 . Wtedy
. Wtedy
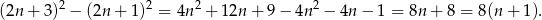
Widać, że jest to liczba podzielna przez 8.
