Zadanie nr 5487256
Udowodnij, że dla każdej liczby naturalnej  , gdzie
, gdzie 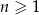 , liczba
, liczba 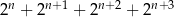 jest podzielna przez 30.
jest podzielna przez 30.
Rozwiązanie
Przekształcamy dane wyrażenie
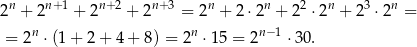
Widać teraz, że jeżeli 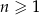 , to liczba ta rzeczywiście dziali się przez 30.
, to liczba ta rzeczywiście dziali się przez 30.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że dla każdej liczby naturalnej  , gdzie
, gdzie 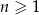 , liczba
, liczba 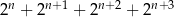 jest podzielna przez 30.
jest podzielna przez 30.
Przekształcamy dane wyrażenie
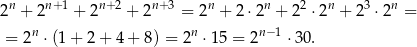
Widać teraz, że jeżeli 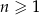 , to liczba ta rzeczywiście dziali się przez 30.
, to liczba ta rzeczywiście dziali się przez 30.
