Zadanie nr 5938836
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 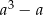 jest podzielna przez 12.
jest podzielna przez 12.
Rozwiązanie
Zauważmy najpierw, że
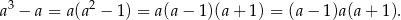
Ponieważ jest to iloczyn trzech kolejnych liczb naturalnych, to liczba ta jest podzielna przez 3 (bo jedna z liczb: 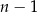 ,
,  lub
lub 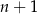 dzieli się przez 3).
dzieli się przez 3).
Ponieważ 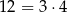 , wystarczy jeszcze udowodnić podzielność przez 4. Wiemy, że liczba
, wystarczy jeszcze udowodnić podzielność przez 4. Wiemy, że liczba  jest nieparzysta, więc możemy ją zapisać w postaci
jest nieparzysta, więc możemy ją zapisać w postaci 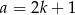 . Wtedy
. Wtedy
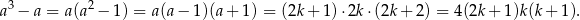
Liczba ta jest oczywiście podzielna przez 4.

