Zadanie nr 6049641
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 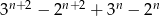 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Rozwiązanie
Przekształcamy dane wyrażenie
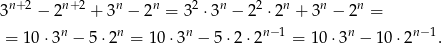
Widać teraz, że oba składniki dzielą się przez 10.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 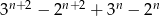 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Przekształcamy dane wyrażenie
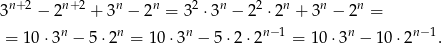
Widać teraz, że oba składniki dzielą się przez 10.
