Zadanie nr 9769644
Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych nieparzystych jest podzielna przez 3.
Rozwiązanie
Trzy kolejne nieparzyste liczby naturalne możemy oznaczyć przez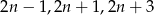 
. Zatem ich suma sześcianów jest równa
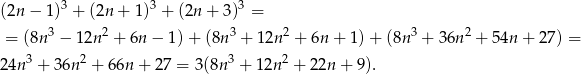
Teraz widać gołym okiem, że powyższa suma jest liczbą podzielną przez 3.
