Zadanie nr 6866597
Podać zaprzeczenie zdania i doprowadzić je do wyrażenia nie zawierającego negacji.
![∀z ∀t∀y [(z + t ≤ y) ∧ cos2 t = 2z]](https://img.zadania.info/zad/6866597/HzadT0x.gif)
Rozwiązanie
Korzystamy z podstawowych praw rachunku zdań
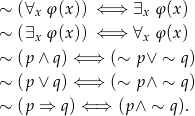
Liczymy
![( ) 2 ∼ ∀z∀t∀y [(z+ t ≤ y)∧ co s t = 2z] ⇐ ⇒ ⇐ ⇒ ∃ ∃ ∃ [∼ (z+ t ≤ y )∨ ∼ (co s2t = 2z)] ⇐ ⇒ z t y ⇐ ⇒ ∃z∃t∃y [z + t > y ∨ cos2t ⁄= 2z ].](https://img.zadania.info/zad/6866597/HzadR1x.gif)
Odpowiedź: ![∃ ∃ ∃ [z + t > y ∨ cos2t ⁄= 2z ] z t y](https://img.zadania.info/zad/6866597/HzadR2x.gif)
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Podać zaprzeczenie zdania i doprowadzić je do wyrażenia nie zawierającego negacji.
![∀z ∀t∀y [(z + t ≤ y) ∧ cos2 t = 2z]](https://img.zadania.info/zad/6866597/HzadT0x.gif)
Korzystamy z podstawowych praw rachunku zdań
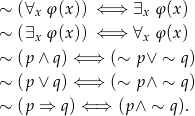
Liczymy
![( ) 2 ∼ ∀z∀t∀y [(z+ t ≤ y)∧ co s t = 2z] ⇐ ⇒ ⇐ ⇒ ∃ ∃ ∃ [∼ (z+ t ≤ y )∨ ∼ (co s2t = 2z)] ⇐ ⇒ z t y ⇐ ⇒ ∃z∃t∃y [z + t > y ∨ cos2t ⁄= 2z ].](https://img.zadania.info/zad/6866597/HzadR1x.gif)
Odpowiedź: ![∃ ∃ ∃ [z + t > y ∨ cos2t ⁄= 2z ] z t y](https://img.zadania.info/zad/6866597/HzadR2x.gif)
