/Szkoła podstawowa/Procenty/W geometrii

Zadanie nr 3222974

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości obu podstaw trapezu wydłużono o 25%. O ile procent należy skrócić jego wysokość aby pole trapezu nie uległo zmianie?

Rozwiązanie

Jeżeli 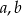a,b są długościami podstaw trapezu, a 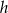h jego wysokością, to pole trapezu przed zmianą jest równe

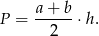
P = a-+-b-⋅h. 2

Jeżeli oznaczymy przez 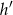′ h taką długość wysokości trapezu, aby po wydłużeniu podstaw pole się nie zmieniło, to mamy równanie

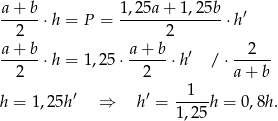
a-+-b-⋅h = P = 1,2-5a+--1,25b ⋅h′ 2 2 a-+-b- a+--b- ′ --2--- 2 ⋅h = 1 ,25⋅ 2 ⋅h / ⋅a+ b h = 1,2 5h′ ⇒ h′ = --1--h = 0,8h. 1,25

Wysokość należy więc skrócić o 20%.  
Odpowiedź: Należy ją skrócić o 20%

Wersja PDF