Zadanie nr 2716275
Boki 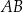 i
i 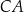 trójkąta
trójkąta 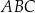 są zawarte w prostych
są zawarte w prostych 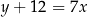 i
i 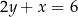 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 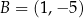 i
i 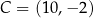 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
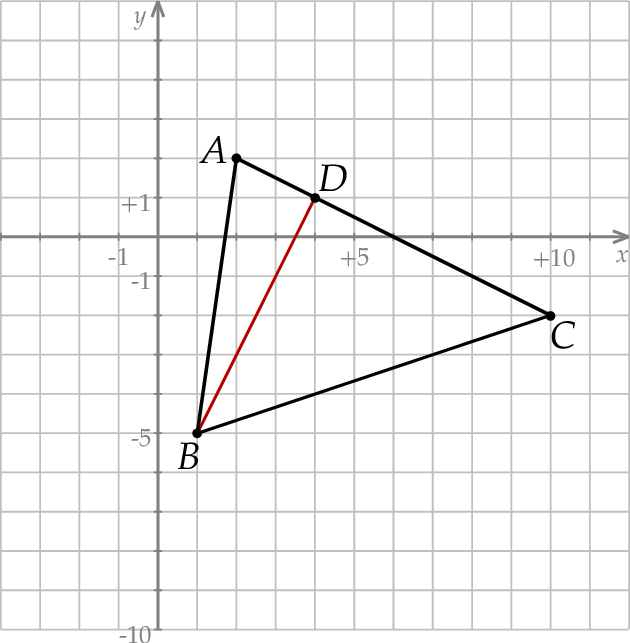
Rozpocznijmy od wyznaczenia współrzędnych wierzchołka 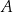 , czyli punktu wspólnego podanych prostych.
, czyli punktu wspólnego podanych prostych.
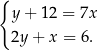
Odejmujemy od drugiego równania pierwsze pomnożone przez 2 (żeby skrócić 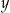 ) i mamy
) i mamy

Stąd 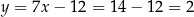 i
i 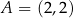 .
.
Sposób I
Aby obliczyć pole trójkąta obliczymy długość wysokości 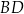 trójkąta
trójkąta 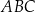 . Prosta
. Prosta 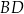 jest prostopadła do prostej
jest prostopadła do prostej 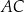 , czyli do prostej
, czyli do prostej 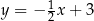 , więc ma równanie postaci
, więc ma równanie postaci 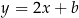 . Współczynnik
. Współczynnik 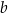 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 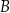 .
.
Wysokość 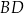 ma więc równanie
ma więc równanie 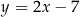 . Szukamy teraz punktu wspólnego
. Szukamy teraz punktu wspólnego 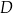 tej wysokości i prostej
tej wysokości i prostej 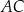 .
.
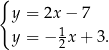
Odejmujemy od pierwszego równania drugie (żeby skrócić 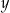 ) i mamy
) i mamy
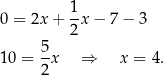
Mamy stąd 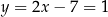 i
i 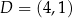 . Liczymy teraz długość podstawy
. Liczymy teraz długość podstawy 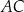 i wysokości
i wysokości 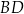 trójkąta.
trójkąta.
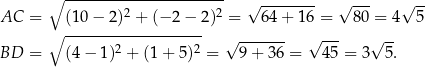
Pole trójkąta jest więc równe
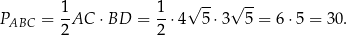
Sposób II
Tym razem skorzystamy ze wzoru na pole trójkąta o wierzchołkach 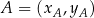 ,
, 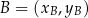 i
i 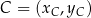 .
.
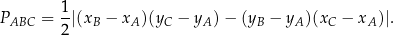
Mamy więc
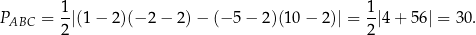
Odpowiedź: 30

