Zadanie nr 2989011
Środek okręgu o równaniu 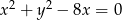 i punkt
i punkt 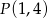 należą do prostej
należą do prostej 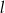 , która przecina okrąg w punktach
, która przecina okrąg w punktach 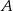 i
i 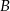 . Oblicz pole trójkąta
. Oblicz pole trójkąta 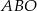 gdzie
gdzie 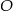 to początek układu współrzędnych.
to początek układu współrzędnych.
Rozwiązanie
Zacznijmy od przekształcenia podanego równania okręgu
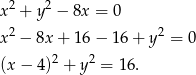
Jest to więc okrąg o środku 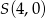 i promieniu 4. Możemy teraz wykonać szkicowy rysunek.
i promieniu 4. Możemy teraz wykonać szkicowy rysunek.
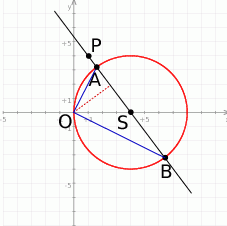
Zastanówmy się co dalej zrobić. Narzucające się dalsze rozwiązanie to wyznaczenie równania prostej 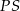 , znalezienie punktów wspólnych
, znalezienie punktów wspólnych 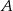 i
i 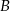 z okręgiem i …. No właśnie i co dalej? Mamy dwie możliwości. Możemy zauważyć, że trójkąt
z okręgiem i …. No właśnie i co dalej? Mamy dwie możliwości. Możemy zauważyć, że trójkąt 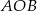 jest trójkątem prostokątnym (kąt
jest trójkątem prostokątnym (kąt 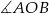 jest oparty na średnicy), a więc do policzenia pola wystarczy znać długości odcinków
jest oparty na średnicy), a więc do policzenia pola wystarczy znać długości odcinków 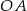 i
i 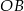 .
.
Drugi sposób jest znacznie prostszy. Do obliczenia pola trójkąta 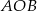 wystarczy znać długości jego podstawy
wystarczy znać długości jego podstawy 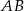 i wysokości opuszczonej na tę podstawę. Ponieważ
i wysokości opuszczonej na tę podstawę. Ponieważ 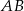 jest średnicą okręgu to znamy jej długość: wynosi 8. Z długością wysokości jest trochę trudniej – jest to odległość punktu
jest średnicą okręgu to znamy jej długość: wynosi 8. Z długością wysokości jest trochę trudniej – jest to odległość punktu 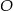 od prostej
od prostej 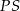 . Tak czy inaczej, jest to bardzo proste rozwiązanie, bo nie musimy wyliczać współrzędnych punktów
. Tak czy inaczej, jest to bardzo proste rozwiązanie, bo nie musimy wyliczać współrzędnych punktów 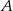 i
i 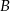 !
!
No to liczymy. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 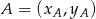 i
i 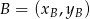 :
:
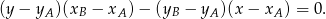
W naszej sytuacji prosta 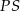 ma równanie
ma równanie
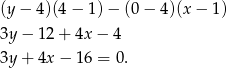
Teraz liczymy odległość tej prostej od punktu 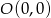 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 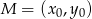 od prostej
od prostej 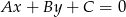 :
:
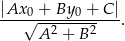
W naszej sytuacji
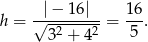
Zatem szukane pole wynosi
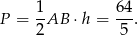
Odpowiedź: