/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Pole

Zadanie nr 3453381

Dodaj do ulubionych
Dodaj do rozwiązanych

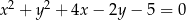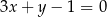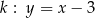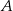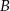Styczne do okręgu o równaniu 2 2 x + y + 4x − 2y − 5 = 0 , które są równoległe do prostej o równaniu 3x + y − 1 = 0 , przecinają prostą k : y = x − 3 w punktach A i B . Oblicz pole trójkąta 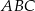ABC , jeśli C = (4,− 7) .

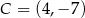Rozwiązanie

Przekształćmy najpierw równanie danego okręgu, tak aby ustalić jaki ma środek i promień

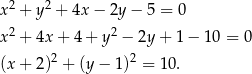
2 2 x + y + 4x− 2y − 5 = 0 x2 + 4x+ 4+ y2 − 2y+ 1− 10 = 0 (x+ 2)2 + (y − 1 )2 = 10.

Jest to zatem okrąg o środku 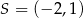S = (− 2,1) i promieniu 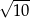√ --- 10 . Możemy zatem zrobić schematyczny rysunek.

PIC

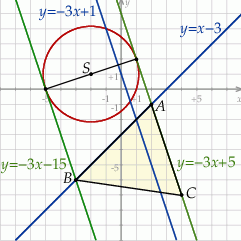
Szukane styczne mają być równoległe do prostej 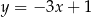y = − 3x + 1 , są zatem postaci 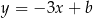y = − 3x+ b . Jest wiele różnych sposobów wyznaczenia współczynnika 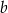b , my pokażemy dwa z nich.

Sposób I

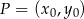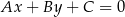Skorzystamy ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

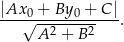
|Ax-0-+-By-0 +-C|- √A--2 +-B-2 .

W naszej sytuacji chcemy aby punkt 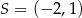S = (− 2,1 ) był w odległości 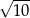√ 10- od prostej 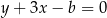y+ 3x− b = 0 . Prowadzi to do równania

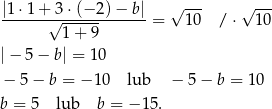
|1 ⋅1 + 3⋅ (− 2)− b | √ --- √ --- -------√------------ = 10 / ⋅ 1 0 1+ 9 |− 5− b| = 10 − 5 − b = − 10 lub − 5 − b = 1 0 b = 5 lub b = − 15.

Są zatem dwie styczne spełniające warunki zadania.

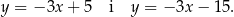
y = − 3x + 5 i y = − 3x − 15 .

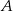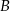Szukamy teraz punktów wspólnych A i B tych stycznych z prostą 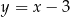y = x− 3 . Najpierw pierwsza styczna

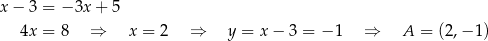
x − 3 = − 3x+ 5 4x = 8 ⇒ x = 2 ⇒ y = x − 3 = − 1 ⇒ A = (2,− 1)

Teraz druga styczna

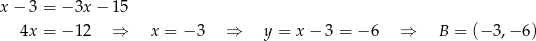
x − 3 = − 3x − 1 5 4x = − 12 ⇒ x = − 3 ⇒ y = x− 3 = − 6 ⇒ B = (− 3,− 6)

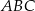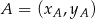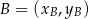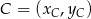Aby obliczyć pole trójkąta ABC , korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

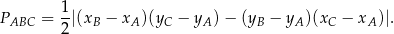
1 PABC = --|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|. 2

W naszej sytuacji

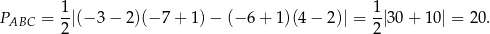
1 1 PABC = 2|(− 3− 2)(− 7+ 1)− (− 6 + 1)(4 − 2)| = 2|30+ 10| = 20.

Sposób II

Szukane styczne mają mieć jeden punkt wspólny z danym okręgiem, tzn. układ równań

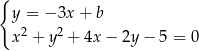
{ y = − 3x + b 2 2 x + y + 4x − 2y − 5 = 0

ma mieć dokładnie jedno rozwiązanie. Układ ten sprowadza się do równania

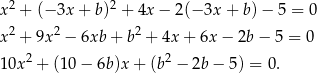
x2 + (− 3x + b)2 + 4x − 2(− 3x + b )− 5 = 0 2 2 2 x + 9x − 6xb + b + 4x + 6x− 2b − 5 = 0 10x 2 + (1 0− 6b )x+ (b2 − 2b− 5) = 0.

Ponieważ równanie to ma mieć dokładnie jedno rozwiązanie, to 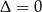Δ = 0 , czyli

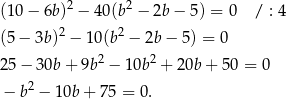
2 2 (10 − 6b ) − 40 (b − 2b − 5 ) = 0 / : 4 (5 − 3b)2 − 10(b 2 − 2b − 5) = 0 2 2 25 − 30b + 9b − 10b + 20b + 50 = 0 2 − b − 10b + 75 = 0.

Rozwiązujemy trzymane równanie kwadratowe.

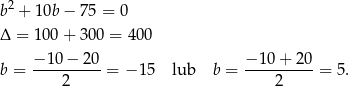
b2 + 10b − 75 = 0 Δ = 100 + 300 = 4 00 b = −-10-−-2-0 = − 15 lub b = −-10+--20-= 5. 2 2

Są zatem dwie styczne spełniające warunki zadania.

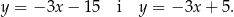
y = − 3x − 15 i y = − 3x + 5 .

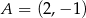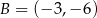Tak samo jak poprzednim sposobie, wyznaczamy teraz A = (2,− 1) i B = (− 3,− 6) . Pole trójkąta obliczymy jednak inaczej – znamy długość podstawy

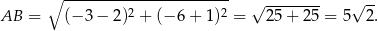
∘ ---------2-----------2- √ -------- √ -- AB = (− 3− 2) + (− 6 + 1) = 25+ 25 = 5 2.

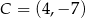Wysokość h opuszczona na tę podstawę to odległość punktu C = (4,− 7) od prostej y− x+ 3 = 0 .

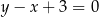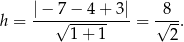
|−-7-−-4-+-3|- -8-- h = √ ------ = √ -. 1 + 1 2

Pole trójkąta 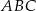ABC jest więc równe

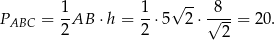
1 1 √ -- 8 PABC = --AB ⋅h = --⋅5 2⋅√----= 20. 2 2 2

 
Odpowiedź: 20

Wersja PDF