Zadanie nr 3549124
Proste 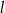 i
i 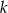 przecinają się w punkcie
przecinają się w punkcie 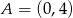 . Prosta
. Prosta 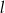 wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu 8, zaś prosta
wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu 8, zaś prosta 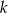 – trójkąt o polu 10. Oblicz pole trójkąta, którego wierzchołkami są: punkt
– trójkąt o polu 10. Oblicz pole trójkąta, którego wierzchołkami są: punkt 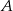 oraz punkty przecięcia prostych
oraz punkty przecięcia prostych 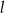 i
i 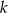 z osią
z osią 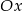 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
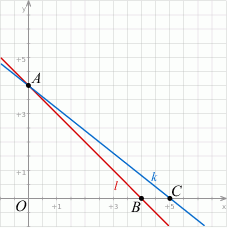
Sposób I
Zauważmy, że pole trójkąta 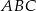 to różnica pól trójkątów
to różnica pól trójkątów 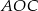 i
i 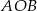 . Zatem
. Zatem
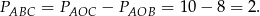
Sposób II
Oba trójkąty 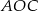 i
i 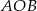 są trójkątami prostokątnymi z przyprostokątną długości
są trójkątami prostokątnymi z przyprostokątną długości  . Z podanych pól mamy więc
. Z podanych pól mamy więc
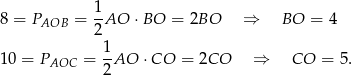
Obliczamy teraz pole trójkąta 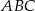 .
.
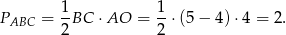
Odpowiedź: 2

