/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Pole

Zadanie nr 3767267

Dodaj do ulubionych
Dodaj do rozwiązanych

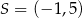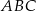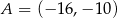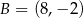Punkt S = (− 1,5 ) jest środkiem okręgu wpisanego w trójkąt ABC , w którym A = (− 16,− 10 ) i B = (8,− 2) . Oblicz pole koła wpisanego w trójkąt ABC .

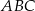Rozwiązanie

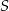Zauważmy najpierw, że promień r okręgu wpisanego w trójkąt, to dokładnie odległość środka S tego okręgu od któregokolwiek z boków.

PIC

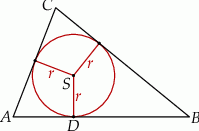
W takim razie musimy obliczyć odległość punktu 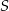S od prostej AB .

PIC

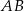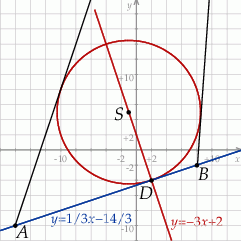
Rozpocznijmy od napisania równania prostej 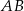AB . Szukamy prostej w postaci 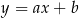y = ax+ b i podstawiamy współrzędne punktów 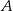A i B .

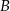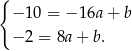
{ − 10 = − 16a+ b − 2 = 8a+ b.

Odejmujemy od drugiego równania pierwsze i mamy

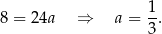
1 8 = 24a ⇒ a = --. 3

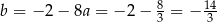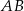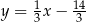Stąd 8 14 b = − 2 − 8a = − 2 − 3 = − 3 i prosta AB ma równanie 1 14 y = 3x − 3 .

Teraz wyznaczymy równanie prostej 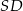SD prostopadłej do 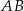AB i przechodzącej przez 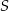S . Jest to prosta postaci 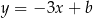y = − 3x+ b . Współczynnik 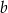b wyznaczamy podstawiając współrzędne punktu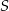 S

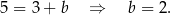
5 = 3+ b ⇒ b = 2.

Prosta 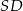SD ma więc równanie 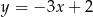y = − 3x + 2 . Wyznaczamy teraz jej punkt wspólny 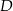D z prostą AB .

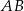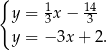
{ y = 1x− 14 3 3 y = − 3x + 2.

Odejmujemy od pierwszego równania drugie i mamy

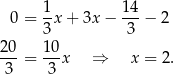
1 14 0 = 3x + 3x − 3--− 2 20-= 10-x ⇒ x = 2 . 3 3

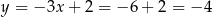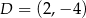Stąd y = − 3x + 2 = − 6+ 2 = − 4 i D = (2,− 4) . Liczymy teraz interesujący nas promień okręgu wpisanego

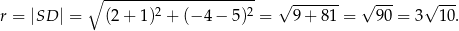
∘ --------------------- √ ------- √ --- √ --- r = |SD | = (2+ 1)2 + (− 4 − 5)2 = 9+ 81 = 90 = 3 10.

Pole koła wpisanego w trójkąt 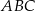ABC jest więc równe

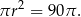
πr 2 = 90π .

 
Odpowiedź: 90π

Wersja PDF