/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Pole

Zadanie nr 5623581

Prosta o równaniu 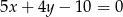5x + 4y− 10 = 0 przecina oś 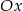Ox układu współrzędnych w punkcie 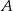A oraz oś 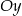Oy w punkcie 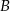B . Oblicz współrzędne wszystkich punktów 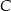C leżących na osi 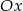Ox i takich, że trójkąt 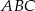ABC ma pole równe 35 .

Wersja PDF

Rozwiązanie

Zacznijmy od schematycznego rysunku.

PIC

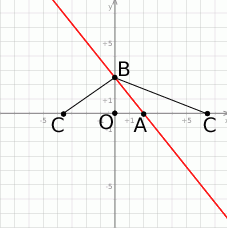
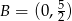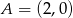Ze wzoru funkcji odczytujemy B = (0, 52) i A = (2,0) . Pole trójkąta 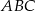ABC możemy obliczyć ze wzoru 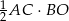1AC ⋅BO 2 . Zatem

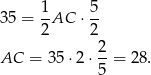
1- 5- 35 = 2 AC ⋅ 2 2 AC = 35 ⋅2 ⋅--= 28. 5

Pozostało znaleźć na osi 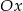Ox punkty 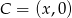C = (x ,0) w odległości 28 od punktu A = (2,0) .

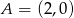Sposób I

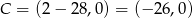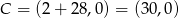Szukane punkty łatwo odgadnąć, są to C = (2 − 28,0) = (− 26 ,0) i C = (2 + 28,0) = (3 0,0) .

Sposób II

Korzystamy ze wzoru na odległość dwóch punktów na płaszczyźnie,

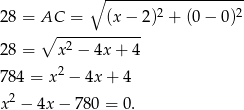
∘ ------------------- 28 = AC = (x− 2)2 + (0− 0)2 ∘ ------------ 28 = x2 − 4x + 4 2 78 4 = x − 4x + 4 x 2 − 4x − 780 = 0.

Dalej

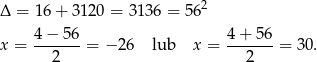
Δ = 16 + 3120 = 3136 = 562 x = 4−--56-= − 2 6 lub x = 4-+-56-= 30. 2 2

 
Odpowiedź: 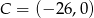C = (− 26,0) lub C = (3 0,0)

Wersja PDF