Zadanie nr 7724907
Dwa boki trójkąta równoramiennego są zawarte w osiach układu współrzędnych, a prosta zawierająca trzeci bok tego trójkąta jest styczna do paraboli o równaniu 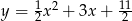 . Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki.
. Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki.
Rozwiązanie
Jeżeli dwa boki trójkąta są zawarte w osiach układu współrzędnych, to mamy do czynienia z trójkątem prostokątnym. Wiemy ponadto, że trójkąt ten ma być równoramienny, więc kąty ostre tego trójkąta muszą być równe 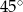 . To oznacza, że przeciwprostokątna trójkąta musi być zawarta w prostej postaci
. To oznacza, że przeciwprostokątna trójkąta musi być zawarta w prostej postaci 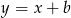 lub
lub 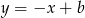 .
.
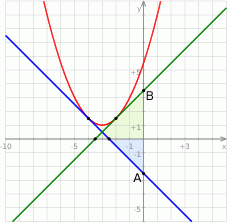
Aby ustalić dla jakich wartości 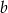 proste tej postaci są styczne do danej paraboli, liczymy pochodną.
proste tej postaci są styczne do danej paraboli, liczymy pochodną.
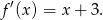
Sprawdzamy teraz w jakich punktach pochodna jest równa 1 lub 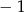
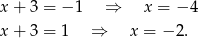
Piszemy teraz równania stycznych do wykresu funkcji 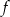 w punktach
w punktach
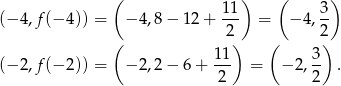
Styczne mają więc odpowiednio równania
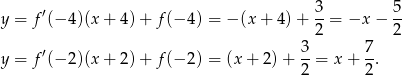
Styczne te przecinają oś 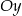 układu odpowiednio w punktach
układu odpowiednio w punktach 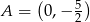 i
i 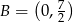 . Zauważmy, że punktów przecięcia z osią
. Zauważmy, że punktów przecięcia z osią 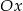 nie musimy wyznaczać, bo interesujące nas trójkąty są równoramienne, więc do obliczenia pola wystarczy nam długość jednej przyprostokątnej. Pola odpowiednich trójkątów są więc równe
nie musimy wyznaczać, bo interesujące nas trójkąty są równoramienne, więc do obliczenia pola wystarczy nam długość jednej przyprostokątnej. Pola odpowiednich trójkątów są więc równe
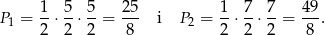
Odpowiedź: 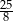 lub
lub