Zadanie nr 8172357
Oblicz pole trójkąta utworzonego przez osie układu współrzędnych i przez prostą o ujemnym współczynniku kierunkowym 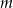 do której należy punkt
do której należy punkt 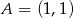 . Dla jakiej wartości
. Dla jakiej wartości 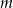 pole tego trójkąta jest najmniejsze?
pole tego trójkąta jest najmniejsze?
Rozwiązanie
Szkicujemy opisaną sytuację.
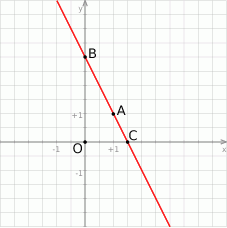
Równanie prostej o współczynniku kierunkowym 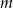 i przechodzącej przez punkt
i przechodzącej przez punkt 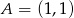 możemy zapisać w postaci
możemy zapisać w postaci
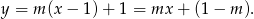
Punkt przecięcia 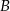 tej prostej z osią
tej prostej z osią 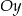 to
to 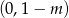 . Wyznaczmy jeszcze punkt
. Wyznaczmy jeszcze punkt 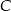 wspólny tej prostej z osią
wspólny tej prostej z osią 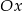 .
.
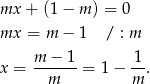
Stąd 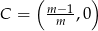 i pole trójkąta, o którym mowa w treści zadania jest więc równe
i pole trójkąta, o którym mowa w treści zadania jest więc równe
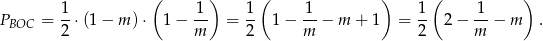
Wyznaczymy teraz najmniejszą możliwą wartość funkcji
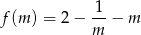
określonej w przedziale 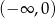 . Liczymy pochodną
. Liczymy pochodną
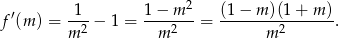
Pochodna jest ujemna w przedziale 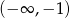 i dodatnia w przedziale
i dodatnia w przedziale 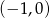 . To oznacza, że w przedziale
. To oznacza, że w przedziale 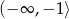 funkcja
funkcja 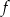 maleje, a w przedziale
maleje, a w przedziale 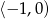 rośnie. W takim razie najmniejszą wartość funkcji otrzymamy dla
rośnie. W takim razie najmniejszą wartość funkcji otrzymamy dla 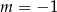 . Pole jest wtedy równe
. Pole jest wtedy równe
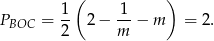
Odpowiedź: 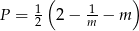 ,
, 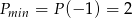 .
.

