Zadanie nr 8256206
Dany jest okrąg o równaniu 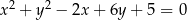 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
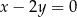 .
. - Oblicz pole trójkąta
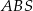 , gdzie
, gdzie 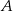 i
i 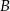 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 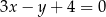 , zaś
, zaś 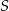 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Rozwiązanie
- Przekształćmy najpierw równanie danego okręgu, tak aby ustalić jaki ma środek i promień
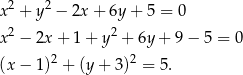
Jest to zatem okrąg o środku
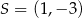 i promieniu
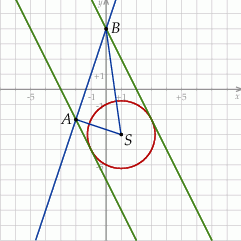
i promieniu 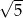 . Możemy zatem zrobić schematyczny rysunek.
. Możemy zatem zrobić schematyczny rysunek. 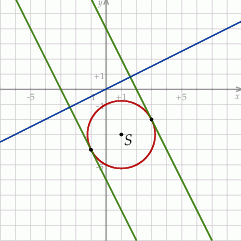
Szukane styczne mają być prostopadłe do prostej
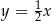 , są zatem postaci
, są zatem postaci 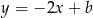 . Jest wiele różnych sposobów wyznaczenia współczynnika
. Jest wiele różnych sposobów wyznaczenia współczynnika 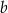 , my pokażemy dwa z nich.
, my pokażemy dwa z nich. Sposób I
Skorzystamy ze wzoru na odległość punktu
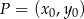 od prostej
od prostej 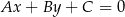 :
: 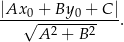
W naszej sytuacji chcemy aby punkt
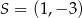 był w odległości
był w odległości 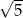 od prostej
od prostej 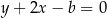 . Prowadzi to do równania
. Prowadzi to do równania 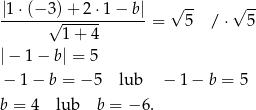
Są zatem dwie styczne spełniające warunki zadania.
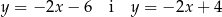
Sposób II
Szukane proste mają mieć jeden punkt wspólny z danym okręgiem, tzn. układ równań
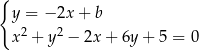
ma mieć dokładnie jedno rozwiązanie. Układ ten sprowadza się do równania
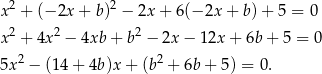
Ponieważ równanie to ma mieć dokładnie jedno rozwiązanie, to
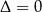 , czyli
, czyli 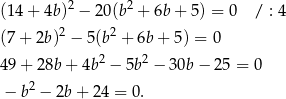
Rozwiązujemy trzymane równanie kwadratowe.
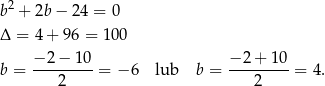
Są zatem dwie styczne spełniające warunki zadania.
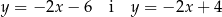
Jeszcze inny, naturalny sposób wyznaczenia
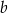 , to wyznaczenie punktów styczności szukanych stycznych z okręgiem (poprzez przecięcie okręgu z prostą równoległą do
, to wyznaczenie punktów styczności szukanych stycznych z okręgiem (poprzez przecięcie okręgu z prostą równoległą do 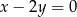 i przechodzącą przez
i przechodzącą przez 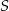 ).
).
Odpowiedź: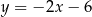 i
i 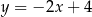
- Szukamy punktów
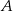 i
i 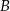
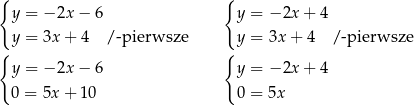
Stąd
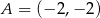 i
i 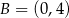 .
. Sposób I
Aby obliczyć pole trójkąta
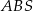 , korzystamy ze wzoru na pole trójkąta o wierzchołkach
, korzystamy ze wzoru na pole trójkąta o wierzchołkach 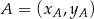 ,
, 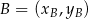 i
i 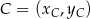 .
. 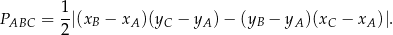
W naszej sytuacji
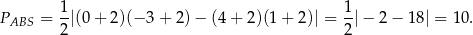
Sposób II
Jeżeli robimy dość dokładne rysunki, to możemy zauważyć, że trójkąt
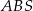 wygląda na prostokątny. Sprawdźmy czy tak jest. Liczymy długości boków tego trójkąta.
wygląda na prostokątny. Sprawdźmy czy tak jest. Liczymy długości boków tego trójkąta. 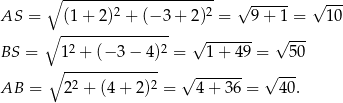
Widać zatem, że
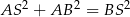 , więc trójkąt jest prostokątny i możemy policzyć jego pole mnożąc długości przyprostokątnych.
, więc trójkąt jest prostokątny i możemy policzyć jego pole mnożąc długości przyprostokątnych. 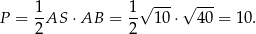
Odpowiedź: 10

