/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Pole

Zadanie nr 8312152

Dodaj do ulubionych
Dodaj do rozwiązanych

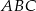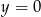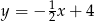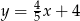Oblicz pole trójkąta ABC , którego boki zawierają się w prostych o równaniach: y = 0 , y = − 12x+ 4 oraz y = 45x + 4 .

Rozwiązanie

Ponieważ jedną z prostych jest oś 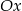Ox , to dwa wierzchołki trójkąta 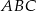ABC wyznaczymy znajdując miejsca zerowe pozostałych dwóch prostych.

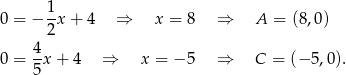
0 = − 1x + 4 ⇒ x = 8 ⇒ A = (8,0) 2 4- 0 = 5x + 4 ⇒ x = − 5 ⇒ C = (− 5,0).

Trzeci wierzchołek trójkąta wyznaczamy szukając punktu wspólnego tych samych prostych.

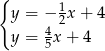
{ y = − 1x + 4 4 2 y = 5x + 4

Odejmujemy od drugiego równania pierwsze i mamy

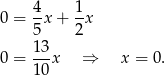
0 = 4-x+ 1x 5 2 13 0 = 10-x ⇒ x = 0.

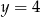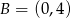Stąd y = 4 i B = (0,4) . Szkicujemy teraz tę sytuację

PIC

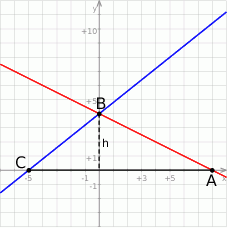
Łatwo teraz obliczyć pole trójkąta 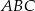ABC .

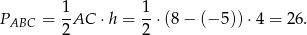
PABC = 1-AC ⋅h = 1-⋅(8 − (− 5)) ⋅4 = 26. 2 2

 
Odpowiedź: 26

Wersja PDF