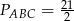Zadanie nr 9247619
Punkty 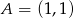 i
i 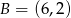 są wierzchołkami trójkąta
są wierzchołkami trójkąta 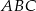 . Wysokości trójkąta
. Wysokości trójkąta 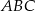 przecinają się w punkcie
przecinają się w punkcie 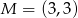 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
Podane informacje pozwalają dość łatwo napisać równania prostych zawierających boki 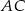 i
i 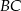 : pierwsza z nich jest prostopadła do
: pierwsza z nich jest prostopadła do 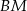 i przechodzi przez
i przechodzi przez 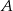 , a druga jest prostopadła do
, a druga jest prostopadła do 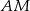 i przechodzi przez
i przechodzi przez 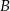 . Aby napisać równania tych prostych skorzystamy ze wzoru na równanie prostej prostopadłej do wektora
. Aby napisać równania tych prostych skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/9247619/HzadR6x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 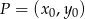
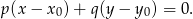
W przypadku prostej 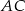 mamy
mamy
![→ −→ v = BM = [3− 6 ,3− 2] = [− 3,1]](https://img.zadania.info/zad/9247619/HzadR10x.gif)
i 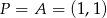 . Prosta
. Prosta 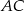 ma więc równanie
ma więc równanie
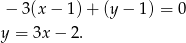
W przypadku prostej 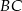 mamy
mamy
![→ −→ v = AM = [3− 1,3− 1] = [2 ,2 ]](https://img.zadania.info/zad/9247619/HzadR15x.gif)
i 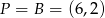 . Prosta
. Prosta 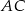 ma więc równanie
ma więc równanie
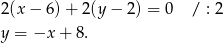
Szukamy teraz punktu wspólnego tych prostych, czyli wierzchołka 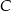 .
.
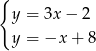
Odejmujemy od pierwszego równania drugie (żeby skrócić 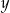 ) i mamy
) i mamy
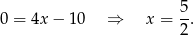
Z pierwszego równania
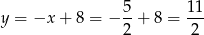
i 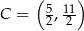 . Pole trójkąta
. Pole trójkąta 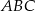 obliczamy ze wzoru na pole trójkąta o wierzchołkach
obliczamy ze wzoru na pole trójkąta o wierzchołkach 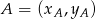 ,
, 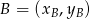 i
i 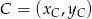 .
.
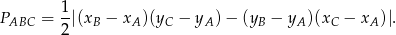
W naszej sytuacji mamy więc
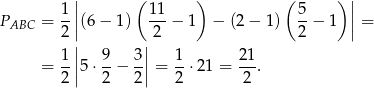
Odpowiedź: