Zadanie nr 9359744
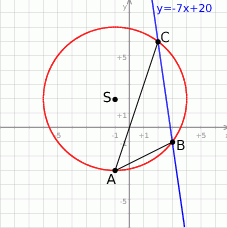
Punkt 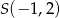 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 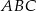 . Wierzchołek
. Wierzchołek 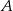 ma współrzędne
ma współrzędne 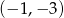 , a bok
, a bok 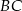 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 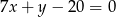 . Oblicz pole trójkąta
. Oblicz pole trójkąta 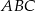 .
.
Rozwiązanie
Skoro znamy środek okręgu opisanego na trójkącie i jeden z jego wierzchołków to możemy napisać równanie okręgu opisanego na trójkącie  .
.
Zacznijmy od wyliczenia promienia.
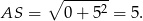
Zatem okrąg opisany ma równanie
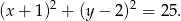
Znajdźmy teraz punkty wspólne tego okręgu z podaną prostą 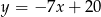 .
.
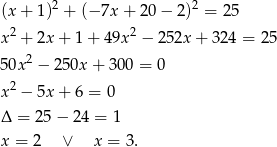
Mamy wtedy odpowiednio 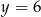 i
i 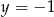 (bo
(bo 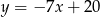 ). Zatem
). Zatem 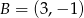 i
i 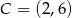 (lub odwrotnie, nie ma to znaczenia).
(lub odwrotnie, nie ma to znaczenia).
Pole trójkąta wyliczymy na dwa sposoby.
Sposób I
Skoro znamy współrzędne wszystkich trzech wierzchołków, możemy skorzystać ze wzoru
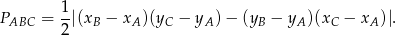
W naszej sytuacji mamy
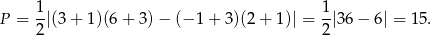
Sposób II
Do wyliczenia pola potrzebujemy długość podstawy i wysokość. Długość podstawy to po prostu długość odcinka 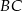 , a wysokość
, a wysokość 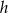 to odległość punktu
to odległość punktu 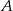 od prostej
od prostej 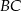 . Liczymy
. Liczymy
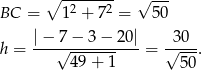
Zatem pole jest równe
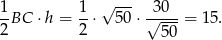
Odpowiedź: 15

