Zadanie nr 9858751
Wierzchołek 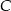 trójkąta
trójkąta 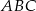 leży na prostej
leży na prostej 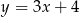 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 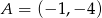 i
i 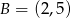 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 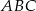 nie zależy od wyboru punktu
nie zależy od wyboru punktu 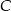 i oblicz to pole.
i oblicz to pole.
Rozwiązanie
Możemy zacząć od rysunku.
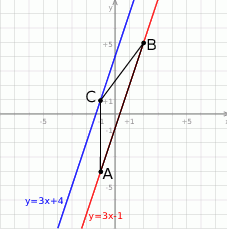
Rysunek sugeruje, że prosta 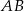 jest równoległa do podanej prostej
jest równoległa do podanej prostej 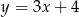 . Jeżeli uda nam się to pokazać, to będzie jasne, że pole trójkąta
. Jeżeli uda nam się to pokazać, to będzie jasne, że pole trójkąta 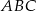 nie będzie zależeć od położenia punkty
nie będzie zależeć od położenia punkty 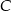 . Pole to będzie równe
. Pole to będzie równe
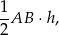
gdzie 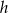 jest odległością między tymi prostymi. Od razu obliczmy
jest odległością między tymi prostymi. Od razu obliczmy
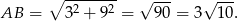
Teraz sprawdzimy, że podana prosta i prosta 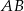 są rzeczywiście równoległe.
są rzeczywiście równoległe.
Sposób I
Napiszmy równanie prostej 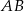 . Szukamy prostej postaci
. Szukamy prostej postaci 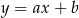 . Wstawiając współrzędne punktów
. Wstawiając współrzędne punktów 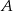 i
i 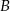 otrzymujemy układ równań.
otrzymujemy układ równań.
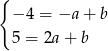
Dodając do drugiego równania pierwsze pomnożone przez 2 (żeby skrócić  ), mamy
), mamy
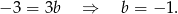
Zatem 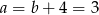 i prosta ta ma równanie
i prosta ta ma równanie 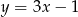 . Rzeczywiście jest więc ona równoległa do prostej zawierającej wierzchołek
. Rzeczywiście jest więc ona równoległa do prostej zawierającej wierzchołek 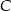 (mają ten sam współczynnik kierunkowy). Policzmy jeszcze odległość między tymi prostymi. Skorzystamy ze wzoru na odległość punktu
(mają ten sam współczynnik kierunkowy). Policzmy jeszcze odległość między tymi prostymi. Skorzystamy ze wzoru na odległość punktu 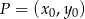 od prostej
od prostej 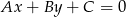 :
:
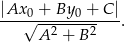
Stosujemy go dla punktu 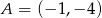 i danej prostej
i danej prostej 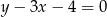 .
.
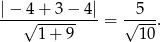
Zatem pole jest równe
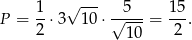
Sposób II
Zamiast wyznaczać równanie prostej 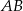 , mogliśmy tylko sprawdzić czy odległość punktów
, mogliśmy tylko sprawdzić czy odległość punktów 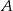 i
i 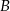 od danej prostej
od danej prostej 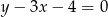 jest taka sama. Liczymy
jest taka sama. Liczymy
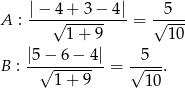
Odległości te są równe, więc proste są równoległe. Pole liczymy jak poprzednio.
Sposób III
Możemy też skorzystać z gotowego wzoru na pole trójkąta o wierzchołkach 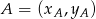 ,
, 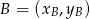 i
i 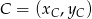 .
.
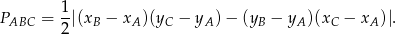
W naszej sytuacji 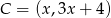 i mamy
i mamy
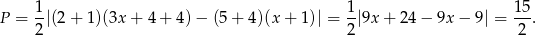
Widać, że liczba ta nie zależy od  , czyli pole nie zależy od wyboru punktu
, czyli pole nie zależy od wyboru punktu 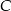 .
.
Odpowiedź: