Zadanie nr 1716516
Końcami odcinka są punkty o współrzędnych 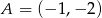 oraz
oraz 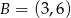 . Odcinek
. Odcinek 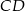 jest obrazem odcinka
jest obrazem odcinka 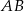 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 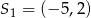 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 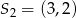 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 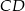 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 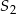 .
.
Rozwiązanie
Zacznijmy od naszkicowania sytuacji.
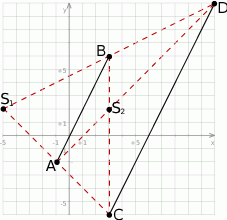
Ponieważ odcinek 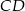 jest obrazem
jest obrazem 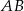 w jednokładności o środku
w jednokładności o środku 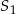 , punkty
, punkty 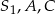 oraz
oraz 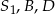 leżą na jednej prostej. Podobnie uzasadniamy, że punkty
leżą na jednej prostej. Podobnie uzasadniamy, że punkty 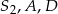 i
i 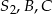 leżą na jednej prostej (przy kolejności punktów ważne jest, że
leżą na jednej prostej (przy kolejności punktów ważne jest, że 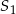 ma skalę dodatnią, a
ma skalę dodatnią, a 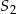 ujemną!). Widzimy zatem jak wyznaczyć punkty C i D – musimy znaleźć punkty wspólne prostych
ujemną!). Widzimy zatem jak wyznaczyć punkty C i D – musimy znaleźć punkty wspólne prostych 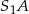 i
i 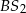 oraz
oraz 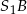 i
i 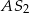 . Aby trochę urozmaicić rozwiązanie, my wyznaczymy w ten sposób tylko współrzędne punktu
. Aby trochę urozmaicić rozwiązanie, my wyznaczymy w ten sposób tylko współrzędne punktu 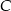 . Potem wyliczymy skalę
. Potem wyliczymy skalę 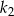 jednokładności o środku
jednokładności o środku 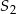 i punkt
i punkt 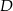 wyznaczymy z równości
wyznaczymy z równości 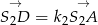 .
.
Aby napisać równania prostych, będziemy korzystać ze wzoru na prostą przechodzącą przez punkty 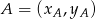 i
i 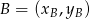 :
:
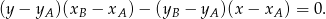
Mamy zatem
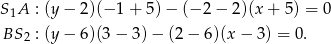
Po uproszczeniu
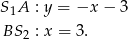
Mamy zatem 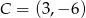 .
.
Aby wyznaczyć skalę podobieństwa 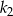 , wyliczamy
, wyliczamy
![→ → S2B = [0,4] ⇒ |S2B| = 4 → → S2C = [0,− 8] ⇒ |S 2C| = 8.](https://img.zadania.info/zad/1716516/HzadR26x.gif)
Zatem 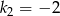 . Punkt
. Punkt 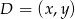 liczymy z równości
liczymy z równości 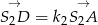 .
.
![→ S2A = [− 4,− 4] → S2D = [x− 3,y − 2].](https://img.zadania.info/zad/1716516/HzadR30x.gif)
Mamy zatem równanie
![[x− 3,y − 2] = − 2[− 4,− 4] = [8 ,8 ].](https://img.zadania.info/zad/1716516/HzadR31x.gif)
Stąd 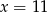 i
i 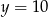 .
.
Odpowiedź: 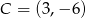 ,
, 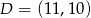 ,
, 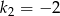 .
.

