Zadanie nr 3077869
Kwadrat o wierzchołkach 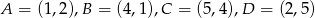 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 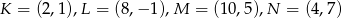 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
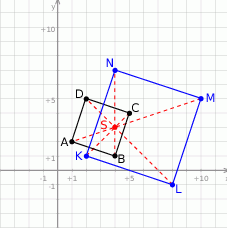
Ustalenie skali to żaden problem: liczymy ile razy zmieniła się długość boku kwadratu.
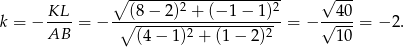
Najważniejsze w tym zadaniu to poprawnie ustalić, które wierzchołki przechodzą na które. Jednokładność przeprowadza odcinek na odcinek równoległy, więc bok 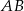 musi przejść na bok
musi przejść na bok 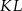 lub na bok
lub na bok 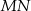 . Ponieważ jednak wiemy, że skala jednokładności jest ujemna, obraz boku
. Ponieważ jednak wiemy, że skala jednokładności jest ujemna, obraz boku 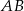 w jednokładności musi być wyżej niż obraz boku
w jednokładności musi być wyżej niż obraz boku 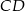 , więc bok
, więc bok 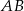 musi przejść na bok
musi przejść na bok 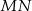 . Co więcej, zwrot wektora
. Co więcej, zwrot wektora 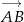 również ulega zmianie przy jednokładności o ujemnej skali, więc punkt
również ulega zmianie przy jednokładności o ujemnej skali, więc punkt 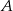 musi przejść na
musi przejść na 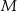 , a punkt
, a punkt 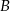 na punkt
na punkt 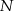 .
.
Teraz wiemy już wszystko, co jest nam potrzebne do wyznaczenia środka jednokładności.
Sposób I
Aby wyznaczyć środek jednokładności wystarczy znaleźć punkt wspólny prostych 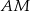 i
i 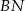 .
.
Równanie prostej 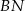 łatwo zgadnąć:
łatwo zgadnąć: 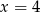 , a równanie prostej
, a równanie prostej 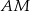 wyznaczamy podstawiając współrzędne punktów
wyznaczamy podstawiając współrzędne punktów 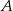 i
i 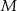 do wzoru
do wzoru 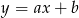 .
.
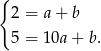
Odejmując od drugiego równania pierwsze (żeby zredukować 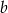 ) mamy
) mamy 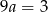 , czyli
, czyli 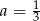 . Zatem
. Zatem 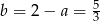 . Pozostało znaleźć punkt wspólny prostych
. Pozostało znaleźć punkt wspólny prostych 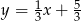 oraz
oraz 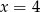 . Podstawiamy
. Podstawiamy 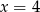 do pierwszego równania
do pierwszego równania
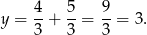
Zatem 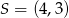 .
.
Sposób II
Skoro wiemy, że punkt 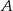 przechodzi na punkt
przechodzi na punkt 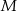 , to wystarczy znaleźć punkt
, to wystarczy znaleźć punkt 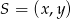 odcinka
odcinka 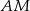 taki, że
taki, że 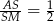 . Najłatwiej zapisać to przy pomocy wektorów.
. Najłatwiej zapisać to przy pomocy wektorów.
![−→ −→ SM = 2 AS [10 − x ,5− y] = 2[x − 1,y− 2] { 10 − x = 2x − 2 ⇒ x = 4 5− y = 2y − 4 ⇒ y = 3.](https://img.zadania.info/zad/3077869/HzadR37x.gif)
Zatem 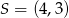 .
.
Odpowiedź: Środek: 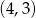 , skala:
, skala: 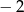 .
.

