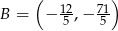/Szkoła średnia/Geometria/Geometria analityczna/Przekształcenia

Zadanie nr 5140703

Dodaj do ulubionych
Dodaj do rozwiązanych

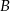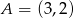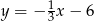Wyznacz współrzędne punktu B , który jest symetryczny do punktu A = (3,2) względem prostej y = − 13x − 6 .

Rozwiązanie

Najpierw wyznaczamy równanie prostej prostopadłej do 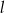l i przechodzącej przez punkt A .

PIC

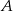Szukamy prostej prostopadłej do do danej prostej, więc musi ona mieć postać 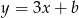y = 3x + b . Współczynnik 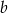b wyznaczamy podstawiając współrzędne punktu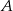 A

2 = 3 ⋅3 + b ⇒ b = − 7.

Zatem prosta 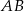AB ma równanie: y = 3x − 7 .

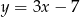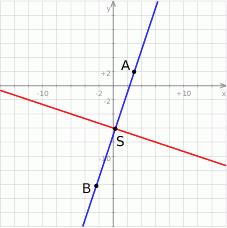
Wyznaczamy punkt 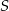S przecięcia się dwóch prostych

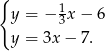
{ y = − 1x − 6 3 y = 3x − 7.

Przyrównujemy do siebie równania i otrzymujemy

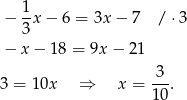
1- − 3 x− 6 = 3x − 7 /⋅ 3 − x − 18 = 9x − 21 3 = 1 0x ⇒ x = 3-. 10

Zatem

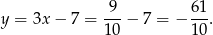
y = 3x − 7 = 9--− 7 = − 6-1. 10 1 0

Wyznaczony przed chwilą punkt 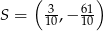( 3- 61) S = 10,− 10 jest środkiem odcinka 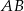AB . Wyznaczamy punkt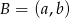 B = (a,b)

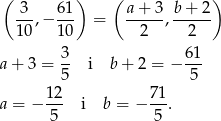
( ) ( ) 3-- 61- a+--3-b-+-2- 10,− 10 = 2 , 2 a+ 3 = 3- i b+ 2 = − 61- 5 5 12- 71- a = − 5 i b = − 5 .

Zatem 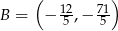( ) B = − 125 ,− 715  
Odpowiedź: ( ) B = − 125 ,− 715

Wersja PDF