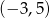/Szkoła średnia/Geometria/Geometria analityczna/Przekształcenia

Zadanie nr 6692120

Dodaj do ulubionych
Dodaj do rozwiązanych

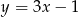Dana jest prosta l o równaniu y = 3x − 1 oraz punkt 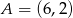A = (6,2) . Wyznacz punkt 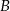B symetryczny do punktu 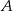A względem prostej l .

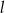Rozwiązanie

Najpierw wyznaczamy równanie prostej prostopadłej do 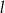l i przechodzącej przez punkt A .

PIC

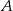Wyznaczamy współczynnik kierunkowy

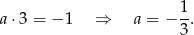
a⋅3 = − 1 ⇒ a = − 1-. 3

Teraz podstawiamy współrzędne punktu 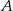A i wyznaczamy wyraz wolny

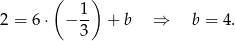
( ) 2 = 6 ⋅ − 1- + b ⇒ b = 4. 3

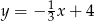Zatem prosta AB ma równanie: y = − 13x + 4 .

Sposób I

Wyznaczamy punkt S przecięcia się dwóch prostych

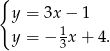
{ y = 3x− 1 y = − 1x+ 4. 3

Przyrównujemy do siebie równania i otrzymujemy

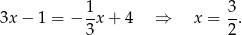
1 3 3x − 1 = − -x + 4 ⇒ x = -. 3 2

Zatem

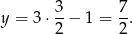
3 7 y = 3 ⋅2-− 1 = 2.

Wyznaczony przed chwilą punkt 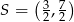( ) S = 3, 7 2 2 jest środkiem odcinka 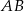AB . Wyznaczamy punkt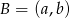 B = (a,b)

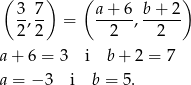
( ) ( ) 3 7 a+ 6 b + 2 -, -- = -----,------ 2 2 2 2 a+ 6 = 3 i b + 2 = 7 a = − 3 i b = 5.

Sposób II

Tym razem skorzystamy ze wzoru na odległość punktu od prostej. Obliczamy odległość punktu 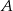A od prostej 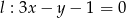l : 3x− y− 1 = 0 (punkt 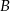B będzie leżeć w tej samej odległości od l )

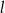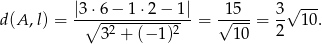
|3⋅ 6− 1⋅2 − 1| 15 3√ --- d(A ,l) = -∘-------------- = √----= -- 10. 32 + (− 1)2 10 2

Wprowadzamy oznaczenie 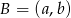B = (a,b) . Wówczas otrzymujemy układ równań

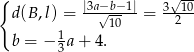
{ |3a−b-−1| 3√10- d (B ,l) = √ 10 = 2 b = − 1a+ 4. 3

Podstawiamy drugie równanie do pierwszego i obliczamy a

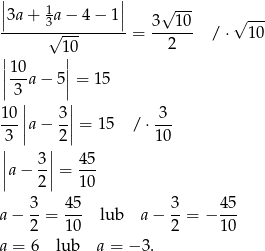
|| 1 || √ --- |3a-+-3a-−-4-−-1| 3--10- √ --- √ --- = 2 / ⋅ 10 | 1|0 ||10- || | 3 a− 5| = 15 || || 10-|a− 3| = 15 / ⋅-3- 3 | 2| 10 || 3 || 45 ||a − --|| = --- 2 10 3- 45- 3- 45- a− 2 = 10 lub a − 2 = − 10 a = 6 lub a = − 3 .

Wartość 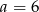a = 6 odpowiada punktowi 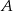A , więc możemy nie liczyć drugiej współrzędnej.

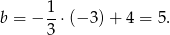
b = − 1-⋅(− 3)+ 4 = 5. 3

 
Odpowiedź: (− 3,5)

Wersja PDF