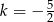/Szkoła średnia/Geometria/Geometria analityczna/Przekształcenia

Zadanie nr 7053227

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest okrąg o1 o równaniu 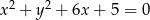2 2 x + y + 6x + 5 = 0 oraz okrąg o2 o równaniu 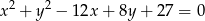x2 + y2 − 12x + 8y + 27 = 0 . Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu 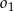o1 jest okrąg o 2 .

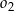Rozwiązanie

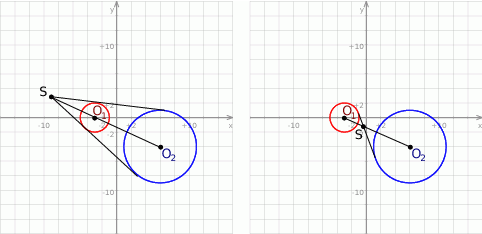
Przekształćmy podane równania okręgów tak, aby było widać jakie są ich środki i promienie.

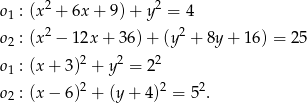
2 2 o1 : (x + 6x + 9) + y = 4 o : (x2 − 12x + 36) + (y2 + 8y + 16 ) = 25 2 o1 : (x + 3)2 + y2 = 22 2 2 2 o2 : (x − 6) + (y+ 4) = 5 .

Widzimy więc, że 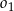o1 jest okręgiem o środku 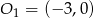O1 = (−3 ,0) promieniu 2, a 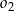o2 ma środek 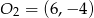O2 = (6 ,−4 ) i promień 5. Możemy zatem naszkicować obydwa okręgi.

PIC

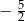Szukana skala podobieństwa wynosi zatem 52 lub − 52 (bo promień zmienia się jak mnożenie przez wartość bezwzględną skali).

Środek jednokładności najłatwiej wyznaczyć posługując się wektorami. Na początku rozważmy przypadek skali 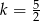5 k = 2 . Szukamy punktu 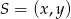S = (x,y) o własności

→ 5 → SO 2 = -SO 1 2 [6 − x ,−4 − y ] = 5[− 3− x,−y ]. 2

Mamy zatem układ równań

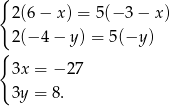
{ 2(6 − x) = 5 (− 3− x ) 2(− 4 − y) = 5(−y ) { 3x = −2 7 3y = 8.

Zatem 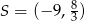S = (− 9, 83) .

Teraz zajmijmy się przypadkiem 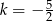k = − 5 2 . Podobnie jak poprzednio mamy

→ 5 → SO 2 = − -SO 1 2 [6 − x ,−4 − y ] = − 5[− 3− x,−y ]. 2

Daje to układ

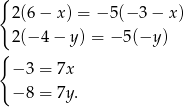
{ 2(6 − x) = −5 (−3 − x ) 2(− 4 − y) = − 5(−y ) { − 3 = 7x − 8 = 7y .

Zatem 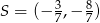3 8 S = (− 7,− 7)  
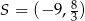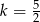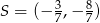Odpowiedź: Środek: S = (− 9, 83) , skala k = 5 2 , lub S = (− 3,− 8) 7 7 i k = − 5 2

Wersja PDF