Zadanie nr 8677667
Okrąg podzielono dwudziestoma punktami na dwadzieścia łuków tej samej długości. Ile można zbudować łamanych zamkniętych z wierzchołkami w tych punktach i z odcinkami równej długości? (Odcinki mogą się przecinać, ale nie mogą się pokrywać.)
Rozwiązanie
Jeżeli ktoś wytrwały, to może sobie wszystkie możliwości narysować, ale my spróbujemy być trochę sprytniejsi (dzięki temu będziemy poradzimy sobie jak odcinków będzie np. 60).
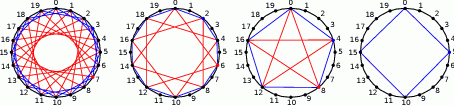
Jak zaczniemy sobie te łamane rysować, to widać, że mogą one być różnej długości. Aby nad tym zapanować, ponumerujmy wierzchołki liczbami od 0 do 19. Zastanówmy się jak wyglądają łamane przechodzące przez wierzchołek z numerem 0. Na pewno jedna z krawędzi o wierzchołku w 0 musi mieć drugi koniec w przedziale 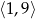 (nie liczymy odcinka 0-10 jako łamanej). Powiedzmy, że ten drugi wierzchołek to
(nie liczymy odcinka 0-10 jako łamanej). Powiedzmy, że ten drugi wierzchołek to  . W takim razie kolejne wierzchołki będą równe
. W takim razie kolejne wierzchołki będą równe 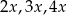 itd., przy czym w momencie, gdy otrzymana liczba przekracza 20, odejmujemy od niej 20 (innymi słowy bierzemy resztę z dzielenia przez 20). Skoro kolejne wierzchołki dane są wzorem
itd., przy czym w momencie, gdy otrzymana liczba przekracza 20, odejmujemy od niej 20 (innymi słowy bierzemy resztę z dzielenia przez 20). Skoro kolejne wierzchołki dane są wzorem 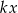 , gdzie
, gdzie 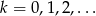 , to łatwo zgadnąć kiedy łamana wróci do punktu wyjścia – tak będzie gdy liczba
, to łatwo zgadnąć kiedy łamana wróci do punktu wyjścia – tak będzie gdy liczba 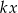 będzie podzielna przez 20. Dla jakiego
będzie podzielna przez 20. Dla jakiego 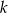 tak będzie? – to zależy od
tak będzie? – to zależy od  .
.
Jeżeli  jest liczbą względnie pierwszą z 20, czyli jedną liczb
jest liczbą względnie pierwszą z 20, czyli jedną liczb 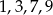 , to
, to 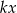 będzie podzielne przez 20 dopiero dla
będzie podzielne przez 20 dopiero dla 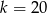 , czyli łamana obejdzie wszystkie wierzchołki. Ponadto dla różnych liczb otrzymamy różne łamane (inna będzie długość jej boku). Są zatem 4 takie łamane (2 z nich są na rysunku).
, czyli łamana obejdzie wszystkie wierzchołki. Ponadto dla różnych liczb otrzymamy różne łamane (inna będzie długość jej boku). Są zatem 4 takie łamane (2 z nich są na rysunku).
Jeżeli  dzieli się przez 2, ale nie dzieli się przez 4, czyli
dzieli się przez 2, ale nie dzieli się przez 4, czyli 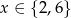 to łamana zamknie się już dla
to łamana zamknie się już dla 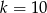 . Innymi słowy, łamana przechodzi przez co drugi wierzchołek. Obie łamane są różne (mają inną długość boku), więc jak dodamy jeszcze dwie analogiczne łamane przechodzące przez wierzchołek 1, to mamy w sumie 4 łamane długości 10.
. Innymi słowy, łamana przechodzi przez co drugi wierzchołek. Obie łamane są różne (mają inną długość boku), więc jak dodamy jeszcze dwie analogiczne łamane przechodzące przez wierzchołek 1, to mamy w sumie 4 łamane długości 10.
Jeżeli  dzieli się przez 4, czyli
dzieli się przez 4, czyli 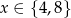 , to mamy łamaną długości 5 (czyli dla
, to mamy łamaną długości 5 (czyli dla 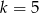 liczba
liczba 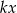 dzieli się przez 20). Teraz otrzymane dwie łamane możemy obrócić na 3 sposoby (żeby przechodziły przez 1,2,3 odpowiednio), więc w sumie mamy 8 łamanych długości 5.
dzieli się przez 20). Teraz otrzymane dwie łamane możemy obrócić na 3 sposoby (żeby przechodziły przez 1,2,3 odpowiednio), więc w sumie mamy 8 łamanych długości 5.
Pozostało nam już tylko 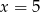 . Wtedy mamy kwadrat i możemy go obrócić na 4 sposoby, co daje nam 5 łamanych.
. Wtedy mamy kwadrat i możemy go obrócić na 4 sposoby, co daje nam 5 łamanych.
W sumie jest więc 4+4+8+5=21 takich łamanych zamkniętych.
Odpowiedź: 21

