/Szkoła średnia/Równania/Układy równań/Liniowy/Z parametrem

Zadanie nr 1855807

Dodaj do ulubionych
Dodaj do rozwiązanych

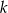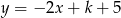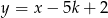Podaj dla jakich wartości parametru k punkt przecięcia się wykresów funkcji y = − 2x + k + 5 i y = x− 5k+ 2 należy do II ćwiartki układu współrzędnych.

Rozwiązanie

Zacznijmy od znalezienia punktu wspólnego podanych prostych, czyli od rozwiązania układu równań

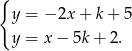
{ y = − 2x + k + 5 y = x − 5k + 2.

Dodajmy do pierwszego równania dwa razy drugie (żeby skrócić x )

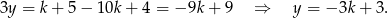
3y = k+ 5− 10k + 4 = − 9k + 9 ⇒ y = − 3k+ 3.

Zatem z drugiego równania

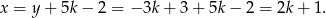
x = y + 5k − 2 = − 3k + 3 + 5k − 2 = 2k+ 1.

Musimy rozwiązać nierówności

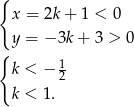
{ x = 2k + 1 < 0 y = − 3k+ 3 > 0 { k < − 1 2 k < 1.

Zatem 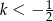1 k < − 2 .  
Odpowiedź: k < − 12

Wersja PDF