/Szkoła średnia/Równania/Układy równań/Liniowy/Z parametrem

Zadanie nr 2912189

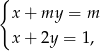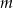Dany jest układ równań { x + my = m x + 2y = 1, gdzie m jest parametrem.

  • Rozwiąż ten układ równań.
  • Określ dziedzinę i naszkicuj wykres funkcji 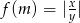f (m ) = |x| y , gdzie para liczb 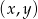(x,y ) jest rozwiązaniem układu.
Wersja PDF

Rozwiązanie

  • Odejmijmy od pierwszego równania drugie (żeby skrócić x ).
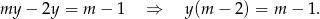
    my − 2y = m − 1 ⇒ y(m − 2) = m − 1.

    Jeżeli 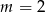m = 2 , to mamy sprzeczną równość 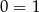0 = 1 i układ nie ma rozwiązań. Jeżeli natomiast 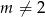m ⁄= 2 to mamy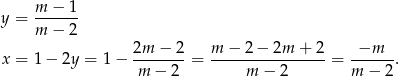

    m-−--1 y = m − 2 2m − 2 m − 2− 2m + 2 −m x = 1− 2y = 1 − ------- = ----------------= ------. m − 2 m − 2 m − 2

     
    Odpowiedź: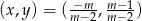 (x,y) = (-−m-, m−1) m −2 m−2

  • Na mocy poprzedniego podpunktu mamy
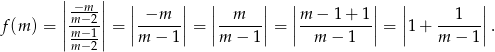
    || −m || | | | | | | | | |m-−2| || -−m---|| ||--m---|| ||m-−-1-+-1-|| || --1---|| f(m ) = ||m-−1|| = | m − 1 | = |m − 1 | = | m − 1 | = |1 + m − 1 |. m −2

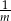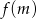    Funkcję homograficzną pod wartością bezwzględną celowo sprowadziliśmy do postaci kanonicznej, aby było łatwo narysować jej wykres – jest to hiperbola m1 przesunięta o wektor [1,1] (po jednej jednostce w górę i w prawo). Aby otrzymać wykres f(m ) trzeba jeszcze odbić część pod osią do góry.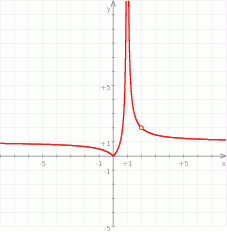

    PIC

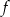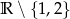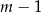    Dziedziną funkcji f jest zbiór R ∖ {1,2} (bo m − 1 jest w mianowniku, a dla 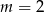m = 2 układ nie ma rozwiązań).

Wersja PDF