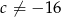Zadanie nr 4584278
Dla jakich współczynników  i
i  układ
układ 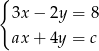
- ma nieskończenie wiele rozwiązań;
- jest sprzeczny?
Rozwiązanie
Sposób I
Spróbujmy rozwiązać ten układ (nie przejmujemy się parametrami). W tym celu do drugiego równania dodajmy pierwsze pomnożone przez 2 (żeby skrócić 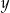 ).
).
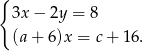
Po pierwsze zauważmy, że to ile układ ma rozwiązań zależy tylko od drugiego równania, czyli od tego ile jest możliwych wartość  – tak jest, bo z pierwszego równania można zawsze jednoznacznie wyliczyć
– tak jest, bo z pierwszego równania można zawsze jednoznacznie wyliczyć 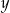 w zależności od
w zależności od  .
.
- Jeżeli układ ma mieć nieskończenie wiele rozwiązań, to nieskończenie wiele rozwiązań musi mieć drugie równanie, czyli
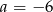 i
i 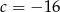 .
.
Odpowiedź: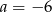 i
i 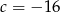
- Jeżeli układ ma być sprzeczny, to sprzeczne musi być drugie równanie, czyli
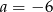 i
i 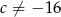 .
.
Odpowiedź: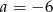 i
i 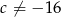
Sposób II
Zadanie możemy rozwiązać metodą wyznacznikową.
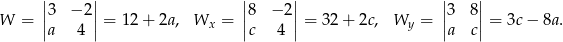
- Jeżeli układ ma mieć nieskończnie wiele rozwiązań, to musimy mieć
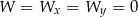 , czyli
, czyli 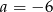 i
i 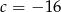 .
.
Odpowiedź: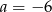 i
i 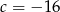
- Jeżeli układ ma być sprzeczny, to musimy mieć
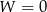 i (
i (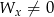 lub
lub 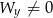 ). Pierwszy warunek oznacza, że
). Pierwszy warunek oznacza, że 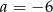 , a drugi daje
, a drugi daje 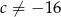 .
.
Odpowiedź: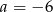 i
i