/Szkoła średnia/Równania/Układy równań/Liniowy/Z parametrem

Zadanie nr 4920695

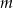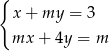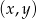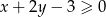Dla jakich wartości parametru m rozwiązaniem układu { x + my = 3 mx + 4y = m jest para liczb (x,y) spełniająca nierówność x + 2y − 3 ≥ 0 ?

Wersja PDF

Rozwiązanie

Zadanie najprościej jest rozwiązać metodą wyznacznikową (można też normalnie, np. z przeciwnych współczynników, ale to tak jakbyśmy udowadniali metodę wyznacznikową – lepiej od razu z niej skorzystać).

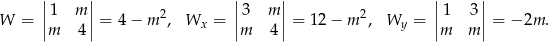
| | | | | | W = ||1 m || = 4 − m 2, W = ||3 m || = 12 − m 2, W = ||1 3 ||= − 2m . |m 4| x |m 4| y |m m |

Jeżeli układ ma mieć jedno rozwiązanie, to musimy mieć 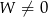W ⁄= 0 , czyli 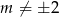m ⁄= ± 2 . Mamy wtedy

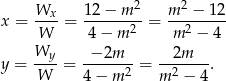
2 2 x = Wx--= 12-−-m-- = m---−-12 W 4 − m 2 m 2 − 4 Wy − 2m 2m y = ----= ------2 = --2----. W 4− m m − 4

Pozostało rozwiązać podaną nierówność

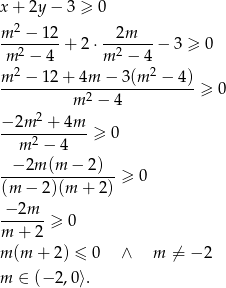
x + 2y− 3 ≥ 0 m-2 −-12 -2m---- m 2 − 4 + 2⋅ m2 − 4 − 3 ≥ 0 2 2 m--−-12-+-4m--−-3(m--−--4)-≥ 0 m 2 − 4 − 2m 2 + 4m ----2-------≥ 0 m − 4 -−-2m-(m-−--2)-- (m − 2)(m + 2) ≥ 0 −-2m--≥ 0 m + 2 m (m + 2) ≤ 0 ∧ m ⁄= − 2 m ∈ (− 2,0⟩.

 
Odpowiedź: m ∈ (− 2,0⟩

Wersja PDF