Zadanie nr 7370352
Dany jest układ równań: 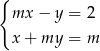 .
.
Dla każdej wartości parametru 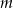 wyznacz parę liczb
wyznacz parę liczb 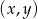 , która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy
, która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy 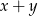 dla
dla 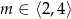 .
.
Rozwiązanie
Aby rozwiązać układ równań mnożymy drugie równanie przez 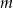 i odejmujemy od niego pierwsze. Otrzymamy
i odejmujemy od niego pierwsze. Otrzymamy 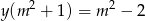 . Stąd łatwo otrzymać, że
. Stąd łatwo otrzymać, że
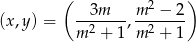
Aby wyznaczyć najmniejszą wartość sumy 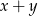 rozważmy funkcję
rozważmy funkcję
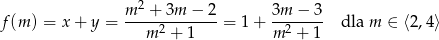
Musimy znaleźć najmniejszą wartość tej funkcji. W tym celu liczymy jej pochodną.
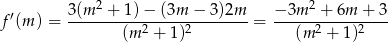
Miejsca zerowe pochodnej to rozwiązania równania 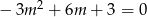 , czyli liczby
, czyli liczby 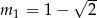 i
i 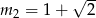 . Jedynie druga z tych liczb leży w interesującym nas przedziale. Musimy jeszcze ustalić jak zmienia się znak pochodnej. Ponieważ mianownik pochodnej jest zawsze dodatni, wystarczy ustalić znak licznika. Ponieważ wykres licznika jest parabolą o ramionach skierowanych w dół - rysunek, więc
. Jedynie druga z tych liczb leży w interesującym nas przedziale. Musimy jeszcze ustalić jak zmienia się znak pochodnej. Ponieważ mianownik pochodnej jest zawsze dodatni, wystarczy ustalić znak licznika. Ponieważ wykres licznika jest parabolą o ramionach skierowanych w dół - rysunek, więc 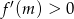 dla
dla 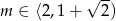 oraz
oraz 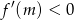 dla
dla 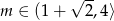 .
.
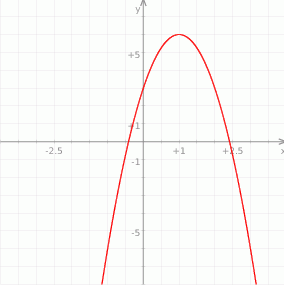
Widzimy zatem, że w punkcie 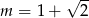 jest lokalne maksimum, a więc najmniejsza wartość
jest lokalne maksimum, a więc najmniejsza wartość 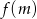 jest w jednym z końców przedziału
jest w jednym z końców przedziału 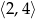 . Ponieważ
. Ponieważ
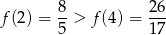
najmniejszą wartością sumy 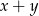 jest
jest 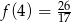
Odpowiedź: 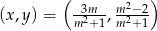 , najmniejsza wartość
, najmniejsza wartość 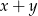 :
: