Zadanie nr 9377182

Dla jakich wartości parametru 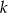rozwiązanie układu równań 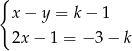{ x − y = k− 1 2x − 1 = − 3− k spełnia warunek |x |+ |y| = 2 + k ?

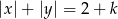Rozwiązanie

Rozwiążmy podany układ równań.

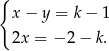
{ x − y = k− 1 2x = − 2− k.

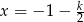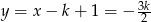Z drugiego równania mamy x = − 1 − k 2 . Podstawiając to do pierwszego równania mamy 3k y = x − k+ 1 = − -2 .

Układ też mogliśmy rozwiązać wyznacznikami:

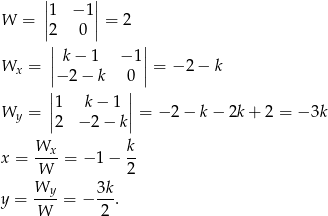
| | W = ||1 − 1|| = 2 |2 0 | || || Wx = | k − 1 − 1|= − 2 − k ||− 2 − k 0| | |1 k − 1 | Wy = || || = − 2 − k− 2k+ 2 = − 3k 2 − 2 − k Wx-- k- x = W = − 1− 2 Wy 3k y = ----= − --. W 2

Mamy zatem równanie

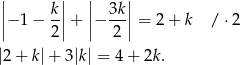
|| || || || |−1 − k|+ |− 3k| = 2 + k / ⋅2 | 2| | 2 | |2 + k|+ 3|k | = 4 + 2k .

Mamy do rozpatrzenia 3 przypadki.

Jeżeli 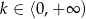k ∈ ⟨0,+ ∞ ) to mamy

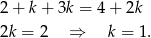
2+ k+ 3k = 4+ 2k 2k = 2 ⇒ k = 1.

Jeżeli 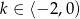k ∈ ⟨− 2,0) to mamy

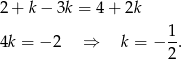
2 + k − 3k = 4+ 2k 1 4k = − 2 ⇒ k = − --. 2

Jeżeli 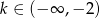k ∈ (− ∞ ,− 2 ) to

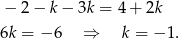
− 2− k − 3k = 4+ 2k 6k = − 6 ⇒ k = −1 .

Rozwiązanie to nie jest zawarte w przedziale 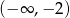(− ∞ ,− 2) .
Odpowiedź: 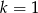k = 1 lub 1 k = − 2