/Szkoła średnia/Geometria/Geometria analityczna/Miejsca geometryczne punktów

Zadanie nr 2838513

Wyznacz figurę, która jest zbiorem środków cięciw paraboli 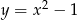2 y = x − 1 przechodzących przez początek układu współrzędnych.

Wersja PDF

Rozwiązanie

Naszkicujmy opisaną sytuację.

PIC

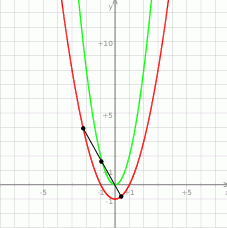
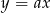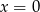Proste przechodzące przez początek układu współrzędnych są postaci y = ax lub x = 0 . Ta druga prosta nie wyznacza cięciwy paraboli, więc wystarczy zajmować się pierwszym przypadkiem. Znajdźmy punkty wspólne tej prostej i paraboli.

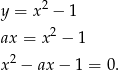
y = x2 − 1 ax = x 2 − 1 2 x − ax − 1 = 0.

Sprawdźmy kiedy to równanie ma rozwiązanie

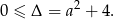
2 0 ≤ Δ = a + 4.

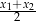Rozwiązanie istnieje więc dla dowolnego a (co oczywiście zgadza się z rysunkiem). Tak naprawdę nie interesują nas te rozwiązania, tylko wyrażenie x1+x-2 2 . Możemy je łatwo wyliczyć ze wzorów Viète’a.

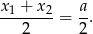
x1 +-x2-= a. 2 2

Wtedy

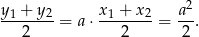
2 y1 +-y-2= a ⋅ x1-+-x2-= a-. 2 2 2

Szukana figura składa się więc z punktów postaci 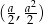a a2 ( 2,2 ) , gdzie 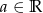a ∈ R . Ze względów estetycznych możemy (ale nie musimy) to rozwiązanie zapisać w postaci y = 2x 2 .  
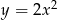Odpowiedź: y = 2x2

Wersja PDF