/Szkoła średnia/Geometria/Geometria analityczna/Miejsca geometryczne punktów

Zadanie nr 6979451

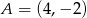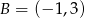Dane są dwa punkty A = (4,− 2) i B = (− 1,3) oraz prosta 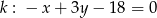k : − x+ 3y − 18 = 0 . Wyznacz współrzędne punktu 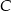C leżącego na prostej 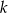k i tak samo odległego od punktów 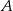A i B .

Wersja PDF

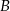Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

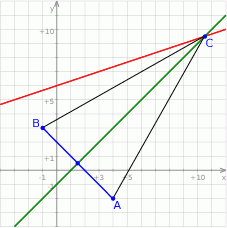
Sposób I

Szukamy punktu 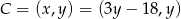C = (x,y) = (3y − 1 8,y) tak, aby spełniona była równość 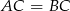AC = BC . Od razu porównujemy kwadraty odległości (żeby nie mieć pierwiastków).

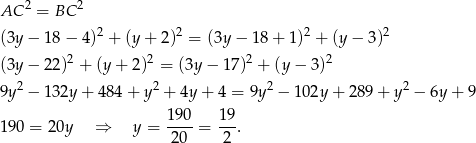
AC 2 = BC 2 2 2 2 2 (3y − 18− 4) + (y + 2 ) = (3y− 18 + 1) + (y− 3) (3y − 22)2 + (y+ 2)2 = (3y − 17)2 + (y − 3)2 9y 2 − 1 32y + 484 + y2 + 4y + 4 = 9y2 − 102y + 289 + y2 − 6y + 9 19 0 19 1 90 = 20y ⇒ y = ---- = ---. 20 2

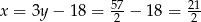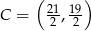Stąd x = 3y − 1 8 = 572 − 18 = 212- i ( ) C = 221, 129 .

Sposób II

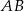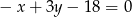Tym razem napiszemy równanie symetralnej odcinka AB i znajdziemy jej punkt wspólny C z daną prostą − x + 3y − 18 = 0 .

Korzystamy ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt (x0,y0)

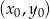
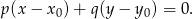
p(x − x0) + q(y − y0) = 0 .

W naszej sytuacji mamy

−→ →v = AB = [− 1 − 4,3 + 2] = [− 5,5],

a punkt to środek odcinka 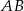AB , czyli

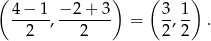
( ) ( ) 4-−-1- −-2+--3 3-1- 2 , 2 = 2,2 .

W takim razie równanie symetralnej jest następujące

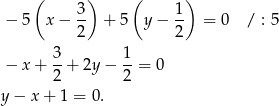
( ) ( ) 3 1 − 5 x − 2- + 5 y− 2- = 0 / : 5 − x+ 3-+ 2y − 1-= 0 2 2 y − x + 1 = 0 .

Szukamy teraz punktu wspólnego tej prostej z daną prostą 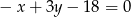− x + 3y − 1 8 = 0 , czyli podstawiamy w powyższym równaniu y = x − 1 .

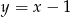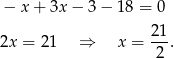
− x + 3x − 3 − 18 = 0 21- 2x = 21 ⇒ x = 2 .

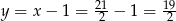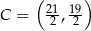Zatem 21 19 y = x − 1 = 2 − 1 = 2 i ( 21- 19-) C = 2 , 2 .  
Odpowiedź: ( ) 21- 19 C = 2 , 2

Wersja PDF