/Szkoła średnia/Geometria/Geometria analityczna/Miejsca geometryczne punktów

Zadanie nr 7862894

Znajdź zbiór środków wszystkich cięciw okręgu 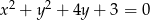2 2 x + y + 4y + 3 = 0 , wyznaczonych przez proste przechodzące przez punkt P = (0,1) .

Wersja PDF

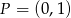Rozwiązanie

Przekształćmy podane równanie okręgu

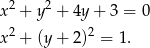
2 2 x + y + 4y+ 3 = 0 x2 + (y+ 2)2 = 1.

Sposób I

Możemy teraz naszkicować rysunek.

PIC

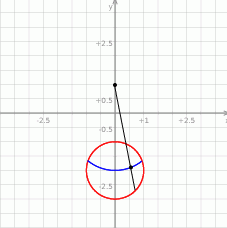
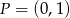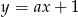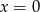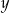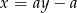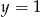Proste przechodzące przez punkt P = (0,1) można zapisać w postaci y = ax+ 1 lub x = 0 . Aby nie mieć dwóch przypadków wygodnie jest jednak te proste zapisać jako funkcje od y ’ka, czyli w nietypowej postaci x = ay− a (tu jest inne a niż poprzednio). Teraz jest lepiej, bo jedyna prosta, która nie jest uwzględniona w tym wzorze, czyli y = 1 nie przecina okręgu. Szukamy punktów wspólnych tej prostej i podanego okręgu.

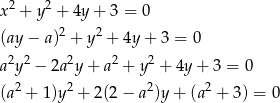
2 2 x + y + 4y + 3 = 0 (ay − a)2 + y2 + 4y+ 3 = 0 a2y2 − 2a2y + a2 + y2 + 4y + 3 = 0 2 2 2 2 (a + 1)y + 2(2− a )y+ (a + 3) = 0

Aby równanie to miało dwa rozwiązania musimy mieć

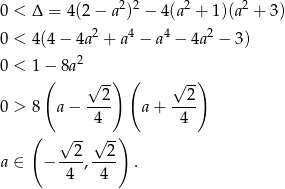
2 2 2 2 0 < Δ = 4(2− a ) − 4 (a + 1 )(a + 3) 0 < 4(4− 4a2 + a4 − a4 − 4a2 − 3) 2 0 < 1− 8a ( √ --) ( √ -) 0 > 8 a − --2- a+ --2- 4 4 ( √ --√ -) ---2 --2- a ∈ − 4 , 4 .

Ponieważ nie interesują nas punkty przecięcia naszej prostej z okręgiem, tylko środek łączącego je odcinka, nie musimy rozwiązywać powyższego równania kwadratowego, tylko możemy wyliczyć 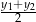y1+y2 2 ze wzorów Viètea.

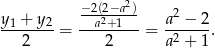
−-2(2−a-2) y-1 +-y-2 --a2+1--- a2 −-2 2 = 2 = a2 + 1.

Mamy wtedy

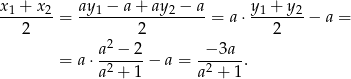
x1-+-x2-= ay1-−-a+--ay2-−-a-= a ⋅ y-1 +-y2-− a = 2 2 2 a2 − 2 − 3a = a⋅ -2----− a = -2----. a + 1 a + 1

 
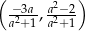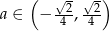
Odpowiedź: ( −3a a2−2 ) a2+1,a2+1 dla ( √2 √2) a ∈ − -4-,-4-

Sposób II

Tym razem trochę dokładniej przyjrzyjmy się naszkicowanemu rysunkowi.

PIC

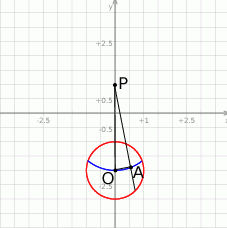
Ponieważ punkt szukany 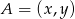A = (x,y) jest środkiem cięciwy, to 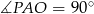∡PAO = 90∘ . Oznacza to, że szukane punkty leżą na okręgu o średnicy 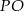P O , czyli na okręgu

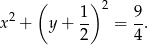
( 1) 2 9 x2 + y+ -- = --. 2 4

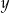Pozostało ustalić jaki dokładnie jest to łuk tego okręgu, to znaczy jak może zmieniać się x lub y . W tym celu sprawdźmy jakie są punkty przecięcia się tych okręgów.

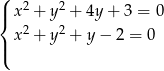
( |{ x2 + y2 + 4y+ 3 = 0 2 2 |( x + y + y− 2 = 0

Odejmując te równania stronami, mamy 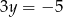3y = − 5 , czyli 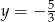5 y = − 3 . Zatem 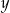y może się zmieniać od 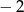− 2 (najniższy punkt na okręgu) do 5 − 3 .

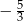Dobrym ćwiczeniem jest sprawdzenie, że otrzymana odpowiedź pokrywa się z tą z poprzedniego sposobu.  
Odpowiedź: 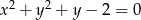x2 + y2 + y − 2 = 0 , dla ⟨ 5) y ∈ − 2 ,− 3

Wersja PDF