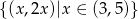Zadanie nr 8344780
Dane są punkty 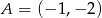 i
i 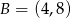 . Wyznacz te punkty prostej
. Wyznacz te punkty prostej 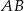 , dla których różnica odległości od punktu
, dla których różnica odległości od punktu 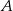 i odległości od punktu
i odległości od punktu 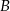 jest większa niż odległość od punktu
jest większa niż odległość od punktu 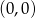 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
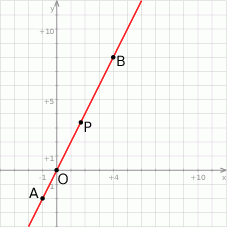
Prosta 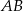 to oczywiście prosta
to oczywiście prosta 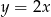 , więc punkty tej prostej mają współrzędne postaci
, więc punkty tej prostej mają współrzędne postaci 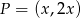 . Musimy zatem rozwiązać nierówność
. Musimy zatem rozwiązać nierówność
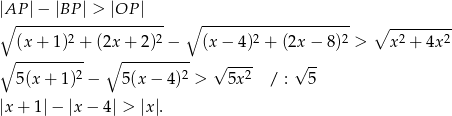
Mamy teraz do rozpatrzenia 4 przypadki.
Jeżeli 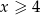 to mamy nierówność
to mamy nierówność
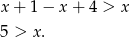
Zatem w tym przypadku 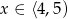 .
.
Jeżeli 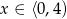 to mamy nierówność
to mamy nierówność
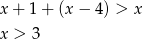
Zatem w tym przypadku 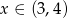 .
.
Jeżeli 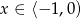 to mamy nierówność
to mamy nierówność
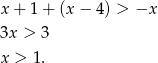
Zatem w tym przypadku nierówność jest sprzeczna.
Jeżeli wreszcie 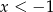 to mamy nierówność
to mamy nierówność
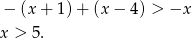
Zatem w tym przypadku nierówność też jest sprzeczna.
Podsumowując otrzymane nierówności mamy 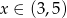 , czyli warunki zadania spełniają punkty postaci
, czyli warunki zadania spełniają punkty postaci
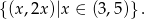
Odpowiedź: