Zadanie nr 8574115
Oblicz, ile jest punktów 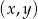 na płaszczyźnie, których współrzędne
na płaszczyźnie, których współrzędne  i
i 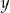 są liczbami całkowitymi spełniającymi odpowiednio nierówności:
są liczbami całkowitymi spełniającymi odpowiednio nierówności: 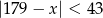 i
i 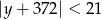 .
.
Rozwiązanie
Dane nierówności możemy zapisać w postaci
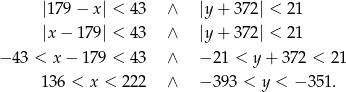
W takim razie  może przyjmować jedną z
może przyjmować jedną z 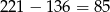 wartości:
wartości:
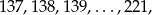
a 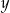 może przyjmować jedną z
może przyjmować jedną z 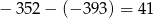 wartości:
wartości:
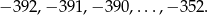
W sumie jest więc
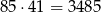
punktów spełniających warunki zadania.
Odpowiedź: 3485

