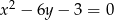/Szkoła średnia/Geometria/Geometria analityczna/Miejsca geometryczne punktów

Zadanie nr 9344791

Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe od okręgu 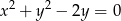x2 + y2 − 2y = 0 i od prostej y + 1 = 0 .

Wersja PDF

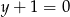Rozwiązanie

PIC

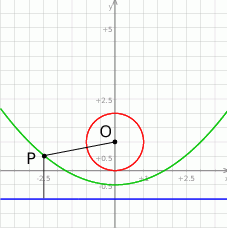
Powiedzmy, że punkt 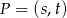P = (s,t) ma żądane własności. Jego odległość od podanej prostej 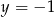y = − 1 to oczywiście

|t− (−1 )| = |t+ 1|

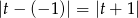
(można też to wyliczyć ze wzoru na odległość punktu od prostej). Aby pozbyć się wartości bezwzględnej zauważmy, że punkt ten nie może leżeć poniżej prostej 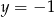y = − 1 . Rzeczywiście, gdyby tak było, to najkrótszy odcinek łączący ten punkt z okręgiem musi przecinać tę prostą, zatem odległóść od prostej byłaby mniejsza niż odległośc od okręgu. W takim razie odległość punktu 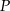P od prostej 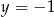y = − 1 jest równa

t+ 1

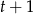
Odległość punktu 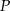P od danego okręgu 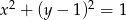2 2 x + (y − 1) = 1 , to długość odcinka 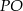PO pomniejszona o promień okręgu, jest ona zatem równa

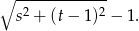
∘ ------------- s2 + (t − 1)2 − 1.

Mamy zatem

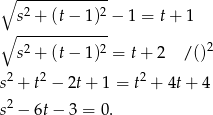
∘ ------------- s2 + (t − 1)2 − 1 = t+ 1 ∘ ------------- s2 + (t − 1)2 = t+ 2 / ()2 2 2 2 s + t − 2t+ 1 = t + 4t + 4 s2 − 6t− 3 = 0.

 
Odpowiedź: x2 − 6y − 3 = 0

Wersja PDF