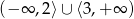/Szkoła średnia/Nierówności/Wielomianowe/Rozwiąż nierówność

Zadanie nr 1972273

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 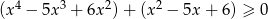4 3 2 2 (x − 5x + 6x )+ (x − 5x + 6) ≥ 0 .

Rozwiązanie

Zapiszmy nierówność w postaci

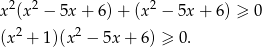
2 2 2 x (x − 5x + 6 )+ (x − 5x + 6) ≥ 0 (x2 + 1)(x2 − 5x + 6) ≥ 0.

Widać teraz, że jeżeli 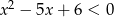x2 − 5x + 6 < 0 to lewa strona nierówności jest ujemna i nierówność jest sprzeczna. Z drugiej strony, jeżeli 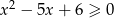2 x − 5x + 6 ≥ 0 to nierówność jest spełniona. Pozostało więc rozwiązać nierówność

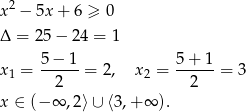
2 x − 5x + 6 ≥ 0 Δ = 25 − 24 = 1 5− 1 5 + 1 x1 = ------= 2, x2 = ------= 3 2 2 x ∈ (− ∞ ,2⟩ ∪ ⟨3,+ ∞ ).

 
Odpowiedź: (− ∞ ,2⟩ ∪ ⟨3,+ ∞ )

Wersja PDF