/Szkoła średnia/Zadania z treścią/Zmiana ilości

Zadanie nr 1042703

Dodaj do ulubionych
Dodaj do rozwiązanych

W chwili początkowej 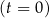(t = 0) masa substancji jest równa 12 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 21% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 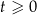t ≥ 0 funkcja 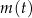m (t) określa masę substancji w gramach po 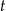t pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 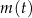m (t) . Oblicz, przez ile pełnych dób masa tej substancji będzie przekraczać 3 gramy.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.