/Szkoła średnia/Zadania z treścią/Zmiana ilości

Zadanie nr 3717537

Czas 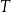T półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 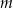m leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą

( 1 ) tT m (t) = m 0 ⋅ -- , 2

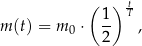
gdzie:
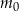m 0 – masa przyjętej dawki leku
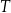T – czas półtrwania leku
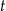t – czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 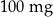100 mg leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 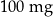100 mg tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 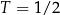T = 1/2 doby.
Oblicz masę leku L w organizmie pana Tomasza tuż przed przyjęciem szóstej dawki tego leku. Wynik podaj w zaokrągleniu do 0,01 mg.

Wersja PDF

Rozwiązanie

Jeżeli obliczamy zawartość leku w organizmie tuż przed przyjęciem 6 dawki, to znaczy, że interesuje nas zwartość leku, która pozostała po przyjęciu 5 dawek po upływie 10 dób. Musimy więc obliczyć sumę

m (5⋅2 )+ m (4 ⋅2)+ m (3⋅2 )+ m (2 ⋅2)+ m (2) = ( ) 5⋅2 ( ) 4⋅2 ( ) 3⋅2 ( ) 2⋅2 ( ) -2 = 100 ⋅ 1- 0,5 + 10 0⋅ 1- 0,5 + 1 00⋅ 1- 0,5 + 100 ⋅ 1- 0,5 + 100 ⋅ 1- 0,5 = 2 2 2 2 2 ( ) = 100 ⋅ -1- + -1- + -1- + 1-+ 1-- . 220 216 2 12 28 24

Suma w nawiasie to suma 5 początkowych wyrazów ciągu geometrycznego z pierwszym wyrazem 1-- a1 = 220 i ilorazem 4 q = 2 = 16 . Suma ta jest więc równa

5 4 5 20 S5 = a1 ⋅ q-−-1-= -1-⋅ (2-)-−-1-= -1-⋅ 2--−-1-= -1-− ---1---. q − 1 220 16 − 1 15 220 15 15⋅ 220

Pozostała dawka leku jest więc równa

( 1 1 ) 20 5 5 100 ⋅ ---− -----20- = ---− ----18 ≈ 6 ,67− ------- ≈ 6,67 mg . 15 15⋅2 3 3 ⋅2 78643 2

 
Odpowiedź: 6,67 mg

Wersja PDF