Zadanie nr 7396032
Dwie partie konserw rybnych, liczące po 1440 konserwy każda, zapakowano w kartony. Każdą z partii zapakowano w ten sposób, że w każdym kartonie znalazła się ta sama liczba konserw, przy czym w przypadku drugiej partii liczbę kartonów zmniejszono o 2 i w kartonach umieszczono o 10 konserw więcej, niż w przypadku kartonów pierwszej partii. Do ilu łącznie kartonów zapakowano te dwie partie konserw?
Rozwiązanie
Sposób I
Jeżeli oznaczymy liczbę kartonów i liczbę konserw w kartonie I partii przez  i
i 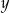 odpowiednio, to mamy układ równań
odpowiednio, to mamy układ równań
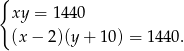
Przekształćmy drugie równanie
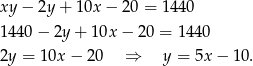
Podstawiamy to wyrażenie do równości 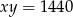 i mamy
i mamy
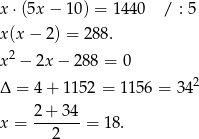
W takim razie konserwy II partii spakowano do 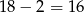 kartonów i w sumie użyto
kartonów i w sumie użyto
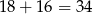
kartonów.
Sposób II
Jeżeli oznaczmy liczbę kartonów w I partii przez  , to w każdym kartonie było
, to w każdym kartonie było 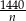 konserw. W przypadku II partii w każdym kartonie było
konserw. W przypadku II partii w każdym kartonie było 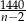 konserw. Z drugiej strony wiemy, w przypadku II partii do każdego kartonu pakowano o 10 konserw więcej. Mamy więc równanie
konserw. Z drugiej strony wiemy, w przypadku II partii do każdego kartonu pakowano o 10 konserw więcej. Mamy więc równanie
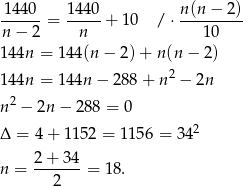
Łącznie użyto więc
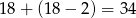
kartonów.
Odpowiedź: 34 kartony.

