/Szkoła średnia/Zadania z treścią/Zmiana ilości

Zadanie nr 8323885

Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po x okresach rozpadu połowicznego wyraża się wzorem (1)x y = 2 .

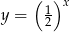W przypadku izotopu jodu 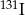131I czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g 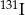131 I nie więcej niż 0,125 g tego pierwiastka.

Wersja PDF

Rozwiązanie

Sposób I

Z podanych informacji wynika, że po 8 dniach z 1 g jodu zostanie 0,5 g jodu. Po kolejnych 8 dniach zostanie 0,25 g jodu, a po kolejnych ośmiu 0,125 g.

Sposób II

Zgodnie z podanym wzorem po x okresach połowicznego rozpadu z 1 g jodu pozostanie

( ) 1- x 2

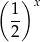
gram jodu. Rozwiązujemy więc nierówność.

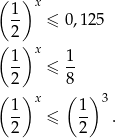
( ) 1 x -- ≤ 0,1 25 ( 2) 1- x 1- 2 ≤ 8 ( ) ( ) 1- x 1- 3 2 ≤ 2 .

Funkcja 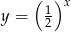( ) 1 x y = 2 jest malejąca, więc mamy stąd 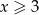x ≥ 3 . Żądaną ilość jodu otrzymamy więc po 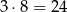3 ⋅8 = 24 dniach.  
Odpowiedź: Po 24 dniach.

Wersja PDF