/Szkoła średnia/Geometria/Planimetria/Wielokąty

Zadanie nr 1775220

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiadomo, że 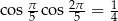π- 2π- 1 cos 5 co s 5 = 4 . Udowodnij, że przekątna pięciokąta foremnego o boku długości 1 ma długość √- 1+--5 2 .

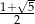Rozwiązanie

Szkicujemy pięciokąt foremny i jego przekątną.

PIC

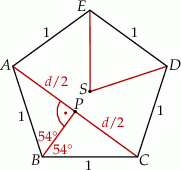
Kąt środkowy 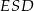ESD ma miarę

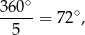
∘ 360-- = 72∘, 5

więc

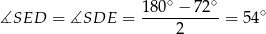
180∘ − 72 ∘ ∡SED = ∡SDE = -----------= 54∘ 2

i kąt wewnętrzny pięciokąta ma miarę

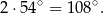
∘ ∘ 2⋅ 54 = 108 .

Jeżeli teraz dorysujemy wysokość 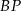BP w trójkącie równoramiennym 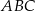ABC oraz oznaczymy 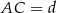AC = d , to

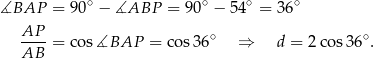
∡BAP = 90∘ − ∡ABP = 90∘ − 54∘ = 3 6∘ AP-- ∘ ∘ AB = cos ∡BAP = co s36 ⇒ d = 2cos 36 .

Pozostało więc obliczyć

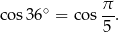
∘ π- cos3 6 = cos 5 .

Jeżeli oznaczymy 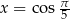x = co s π 5 , to równość daną w treści zadania możemy zapisać w postaci

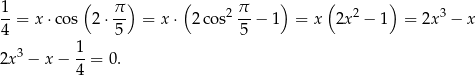
1- ( π-) ( 2 π- ) ( 2 ) 3 4 = x ⋅cos 2⋅ 5 = x ⋅ 2cos 5 − 1 = x 2x − 1 = 2x − x 1 2x 3 − x − --= 0. 4

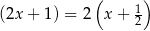Łatwo teraz zauważyć, że jednym z pierwiastków tego równania jest x = − 12 . Dzielimy więc trójmian z lewej strony równania przez ( 1) (2x + 1) = 2 x+ 2 . My zrobimy to grupując wyrazy.

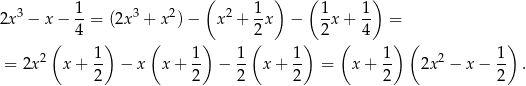
( ) ( ) 3 1- 3 2 2 1- 1- 1- 2x − x − 4 = (2x + x )− x + 2x − 2x + 4 = ( ) ( ) ( ) ( ) ( ) = 2x2 x + 1- − x x + 1- − 1- x + 1- = x + 1- 2x2 − x − 1- . 2 2 2 2 2 2

Oczywiście 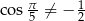π- 1 cos 5 ⁄= − 2 , więc liczba ta jest pierwiastkiem równania

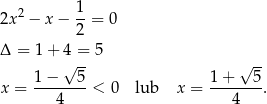
1 2x2 − x− --= 0 2 Δ = 1 + 4 = 5 1 − √ 5- 1 + √ 5- x = --------< 0 lub x = --------. 4 4

Stąd 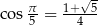π- 1+√-5 co s5 = 4 , czyli

√ -- √ -- d = 2 cos π = 2⋅ 1+----5-= 1-+---5-. 5 4 2
Wersja PDF