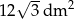/Szkoła średnia/Geometria/Planimetria/Wielokąty

Zadanie nr 2111107

Dodaj do ulubionych
Dodaj do rozwiązanych

Na sześciokącie foremnym opisano okrąg i w ten sześciokąt wpisano okrąg. Pole powstałego pierścienia jest równe 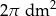2π dm 2 . Oblicz pole powierzchni wielokąta.

Rozwiązanie

Sześciokąt składa się z sześciu przystających trójkątów równobocznych, oznaczmy ich bok przez a .

PIC

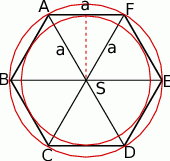
Jeżeli narysujemy sobie obrazek, to widać, że promień okręgu opisanego na sześciokącie jest równy a , a promień okręgu wpisanego to wysokość trójkąta równobocznego, czyli jest równy 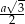a√-3 2 . Mamy więc równanie (liczymy pole pierścienia)

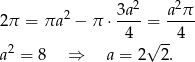
2 2 2π = πa2 − π ⋅ 3a--= a-π- 4 √ --4 a2 = 8 ⇒ a = 2 2.

Zatem pole pojedynczego trójkąta równobocznego wynosi

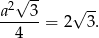
-- a2√ 3 √ -- ------= 2 3. 4

Pole sześciokąta jest 6 razy większe, czyli wynosi 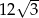√ -- 12 3 .  
Odpowiedź: √ -- 2 12 3 dm

Wersja PDF